Catalyseur optimal : une nouvelle contribution d’IFPEN pour des formules innovantes

Fort d’un important travail de recherche dans le domaine de la catalyse, IFPEN a beaucoup contribué à la mise au point et à la théorisation de formules catalytiques nécessaires au développement de procédés chimiques innovants. En démontrant qu’il est possible de prévoir la valeur du descripteur du catalyseur optimal pour une réaction donnée, ses équipes ont récemment apporté de nouveaux éléments de réponse dans la compréhension du fonctionnement des catalyseurs hétérogènes. 

La recherche combinatoire en catalyse : le hasard pour une nécessité

L’innovation en catalyse est une composante amont cruciale du développement de procédés innovants en chimie, à finalité synthétique (production de molécules) aussi bien qu’énergétique. C’est pourquoi IFPEN maintient dans ce domaine une forte activité tant en recherche fondamentale qu’appliquée.

Pour une réaction donnée, le catalyseur le plus compétitif est généralement le plus actif, c’est-à-dire capable de favoriser la transformation du plus grand nombre de molécules de réactifs par unité de temps et par site actif dans des conditions opératoires données. Un catalyseur est donc caractérisé par une grandeur mesurable, appelé activité, relié à cette fréquence intrinsèque, à la composition du catalyseur et à sa structure locale.

Le chimiste formule, c’est-à-dire qu’il tâche de combiner les éléments du tableau périodique pour obtenir un composé possédant la ou les propriétés recherchées. Le nombre de telles combinaisons étant immense, cette exploration ne peut être efficace sans guides théoriques et sans méthode. C’est particulièrement vrai en catalyse. Les formules bien établies actuellement pour les grandes réactions industrielles ont été le fruit de coûteuses et très longues démarches de type « essais et erreurs », guidées au mieux par l’intuition, ou de découvertes fortuites.

Du principe de Sabatier aux « courbes en volcan » : la science en marche vers l’énergie du futur

Paul Sabatier (prix Nobel de Chimie en 1912 pour ses travaux en catalyse d’hydrogénation et déshydrogénation des molécules organiques) formula son célèbre principe dès le début du XX^e siècle, lequel « stipulait » déjà qu’un catalyseur optimal est celui qui engage une interaction de force intermédiaire avec les réactifs, suffisante pour activer ces derniers et donc favoriser la réaction thermodynamiquement possible, mais insuffisante pour empoisonner les sites actifs par formation de combinaisons trop stables [1]. 

Ce principe inaugurait le concept précieux de « courbe en volcan », corrélation décrivant une série catalytique homologue dans lequel les activités mesurées sont portées en ordonnées, en fonction d’une grandeur, appelée « descripteur », mesurant une énergie d’interaction entre sites et réactifs.

Les progrès récents de la chimie théorique quantique, alliés à la croissance exponentielle de la puissance de calcul numérique disponible à coût constant, ont permis de proposer des descripteurs pertinents et de dégager de nombreuses courbes en volcan pour les principales réactions d’intérêt socio-économique. Outre l’identification des descripteurs de catalyseurs optimaux pour ces réactions, ces évolutions ont stimulé et focalisé les efforts de mise au point.
 
La recherche au sein d’IFPEN a été en pointe dans ce domaine dès les années 1990, démontrant en particulier que les formules des catalyseurs industriels hétérogènes d’hydrodésulfuration, basées sur des sulfures mixtes de molybdène et cobalt ou nickel largement utilisés par le raffinage mondial, sont proches de l’optimum de courbes en volcan [2]. 

Un article très cité paru en 2003 [3] a théorisé ce résultat et l’a étendu à d’autres réactions du domaine du raffinage et de la pétrochimie. Les descripteurs proposés — énergies de liaisons représentatives des interactions entre substrats réactifs et catalyseurs solides, issues de calculs ab initio de coût très modéré — avaient déjà permis d’évaluer l’intérêt en hydrotraitement de sulfures complexes, en incorporant plusieurs éléments de transition ainsi que divers alliages multi-métalliques pour d’autres réactions.

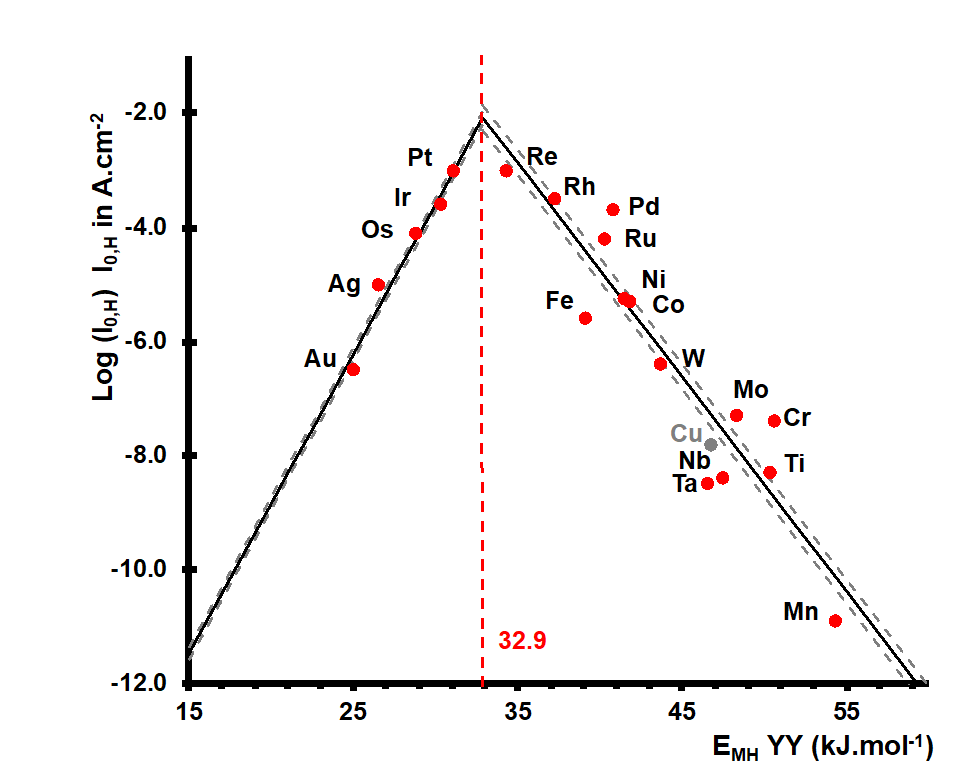
La publication de 2020 [4] a revisité cette théorie en l’appliquant à une plus large gamme de réactions des domaines des nouvelles technologies de l’énergie (électrocatalyse et photocatalyse notamment). La figure 1 présente ainsi un exemple historique de courbe en volcan, revisité par nos soins : il concerne l’effet catalytique du métal de transition utilisé comme cathode sur la vitesse de production d’hydrogène moléculaire par électrolyse de l’eau.
 

Vers une compréhension nouvelle des fondements de la catalyse : la contribution d’IFPEN

Cependant, une question importante restait  ouverte : est-il possible de prévoir la valeur du descripteur du catalyseur optimal pour une réaction donnée ? Si oui, le criblage in silico de champs compositionnels des catalyseurs pourrait être mené avec un minimum de données expérimentales, voire sans aucune, avant d’engager un programme de préparations et tests en laboratoire. 

Cette question générale relève des fondements de notre compréhension de la catalyse. L’article publié en 2020 [4] y apporte pour la première fois une réponse affirmative, étayée expérimentalement et soutenue par une explication théorique cohérente.

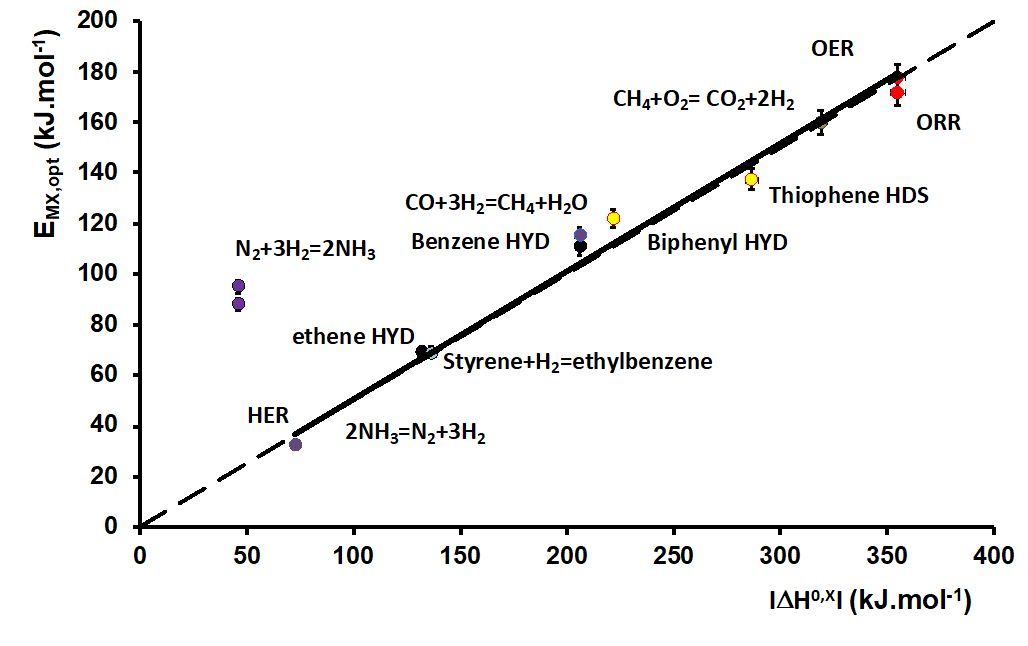
Une réaction donnée étant caractérisée énergétiquement par l’enthalpie standard de réaction DH°, très documentée expérimentalement ou aisément calculée théoriquement, il paraissait naturel de rapprocher ces énergies des énergies EMX,opt décrivant les catalyseurs optimaux pour les mêmes réactions. Le résultat obtenu est présenté figure 2 : une proportionnalité rigoureuse est observée, avec une pente ½ pour 12 réactions très différentes. Cette figure établit donc une relation entre thermodynamique et cinétique des réactions chimiques.
 

L’article IFPEN [4] en apporte l’explication théorique : sous une hypothèse assez générale, il y est démontré que le catalyseur optimal est celui qui aplanit les niveaux d’énergie de tous les intermédiaires en phase adsorbée le long du chemin réactionnel reliant réactifs et produits. L’énergie d’activation de l’étape élémentaire cinétiquement limitante de ce chemin réactionnel est nécessairement minimale pour ce catalyseur optimal, ce qui en fait le plus actif. 

Ce résultat fondamental reconsidère notre compréhension du fonctionnement des catalyseurs hétérogènes. Il est en principe transposable aux catalyses moléculaires et enzymatiques. Sur le plan concret, il autorisera en principe une accélération très significative de la recherche exploratoire en catalyse. 

Références :

[1] P. Sabatier, Berichte der Deutschen Chemischen Gesellschaft, 1911, 44, 1984.
[2] Pour un historique détaillé voir le chapitre I, Catalysis by Transition Metal Sulfides, from Molecular Theory to Industrial Application, ed. H. Toulhoat and P. Raybaud, Éditions Technip, Paris, 2013. ISBN : 9782710809913
[3] H. Toulhoat, P. Raybaud, J. Catal., 2003, 216, 63.
https://doi.org/10.1016/S0021-9517(02)00118-5  
[4] H Toulhoat, P Raybaud, Catalysis Science & Technology, 2020, 10 (7), 2069-2081. https://doi.org/10.1039/C9CY02196E