21.01.2021
4 minutes de lecture
Afin de réduire les temps de calculs jusqu’ici nécessaires pour optimiser des systèmes complexes tels que les machines électriques ou les éoliennes flottantes, les chercheurs IFPEN ont exploré de nouvelles solutions d’optimisation basées sur des surfaces de réponse de type « processus Gaussien » avec variables discrètes. En particulier, ils ont pu réduire le nombre de simulations et aboutir aux résultats optimaux en s’appuyant sur des méthodes plus efficaces : EGO (Efficient Global Optimization) et MADS (Mesh Adaptive Direct Search).
L’optimisation des systèmes complexes : un problème de coût
La conception des systèmes complexes développés par IFPEN (machines électriques, éoliennes flottantes et leurs différents composants) nécessite la résolution de problèmes d’optimisation. Cette résolution peut dépendre de variables discrètes - comme par exemple un nombre de composants (variables entières), des matériaux différents (variables catégorielles, généralement non ordonnées), la présence ou non de certains composants (variables binaires) - en plus de variables à valeurs continues décrivant les dimensions ou propriétés des différents composants.
Au cours de leurs travaux, les équipes d’IFPEN se sont aussi intéressées aux modèles dits «d’ingénierie» qui, bien que dépendants d’un nombre limité de variables d’intérêt (typiquement moins de 20), nécessitent la résolution d’équations complexes intégrées dans des simulateurs coûteux en temps de calcul (jusqu’à plusieurs heures de calcul pour l’évaluation d’une configuration donnée).
Réduire le nombre de simulations avec la méthode EGO adaptée aux variables mixtes
Pour résoudre ce type de problème, l’intérêt des chercheurs IFPEN s’est porté en particulier sur les méthodes d’optimisation basées sur des surfaces de réponse de type « processus Gaussien », dont la variabilité est déterminée par le choix d’une fonction de covariance.
Ces méthodes offrent l’avantage d’être « économiques », car elles requièrent un nombre de simulations moindre pour aboutir à l’approximation de la configuration optimale. Un exemple est la méthode séquentielle EGO (Efficient Global Optimization) qui a été étendue au traitement de « variables mixtes », c’est-à-dire lorsque le vecteur de variables contient à la fois des variables continues et discrètes [1].
Pour cela, des surfaces de réponse ont été intégrées avec des noyaux permettant de capturer à la fois la variabilité et les corrélations de la fonction optimisée, en fonction de l’ensemble des variables : continues ou discrètes, notamment catégorielles.
MADS, une méthode directe en renfort
Une attention particulière a été portée à la résolution des sous-problèmes de la méthode EGO qui sont associés au choix des nouvelles simulations destinées à enrichir la surface de réponse. A cette fin, la méthode directe MADS (Mesh Adaptive Direct Search) a été couplée avec une exploration aléatoire de l’espace des variables catégorielles, en se basant sur une distribution de probabilité apprise et mise à jour au fur et à mesure de l’acquisition de données simulées.
Cette approche, comparée à des méthodes de l’état de l’art, a démontré son efficacité, à savoir sa capacité à, d’une part, explorer le domaine des variables catégorielles en demandant moins de simulations (figure) et, d’autre part, obtenir des résultats d’optimisation peu sensibles au choix des points initiaux.
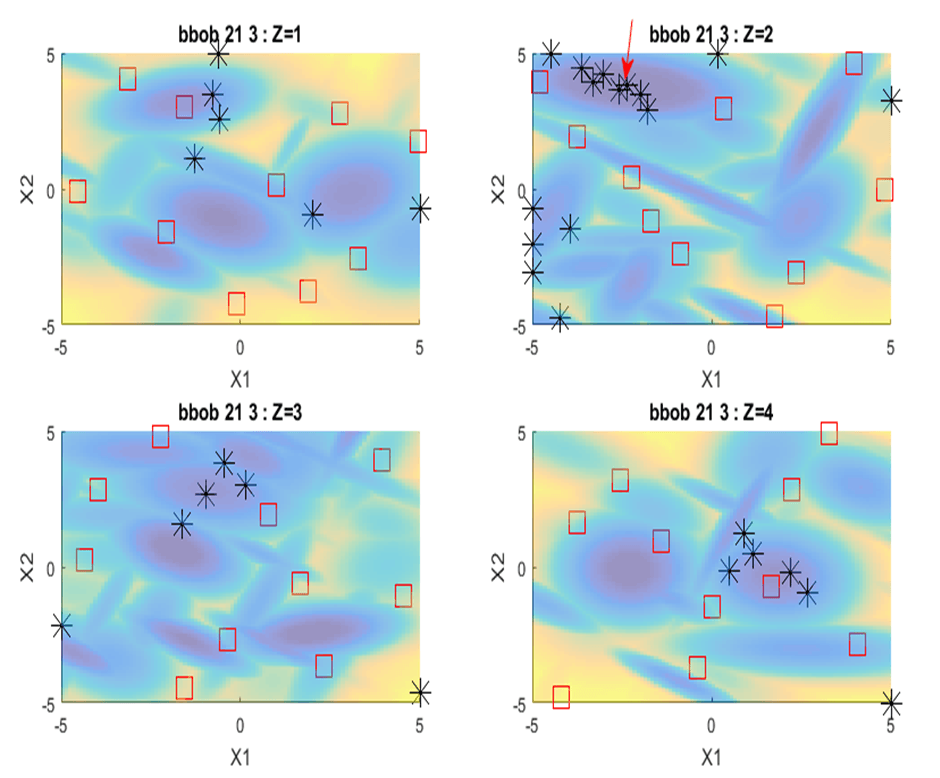
Les couleurs indiquent les niveaux de la fonction à minimiser (la flèche rouge indique la localisation de l’optimum global, associé à la catégorie 2). Les carrés rouges indiquent les simulations du plan d’expérience initial et les croix noires les simulations ajoutées par la méthode.
Ces travaux seront poursuivis et complétés par d’autres approches dans le cadre de nouvelles actions de recherche, aussi bien en interne IFPEN [2] qu’en mode collaboratif : avec le soutien de l’ANR [3], au sein d’un consortium de recherche [4] et au travers d’une collaboration avec Polytechnique Montréal [5].
Références
[1] Munoz Zuniga M. and Sinoquet D., Global Optimization for mixed categorical-continuous variables based on Gaussian process models with a randomized categorical space exploration step, 2020, INFOR, Information Systems and Operational Research, https://doi.org/10.1080/03155986.2020.1730677
[2] Projet DeTOCS : DEsign Tools for Optimization and Control of complex Systems
[3] Projet Samourai (2021-2025) : Simulation Analytics and Meta-model-based solutions for Optimization, Uncertainty and Reliability AnalysIs, avec CEA, Supelec, EDF, EMSE, IFPEN, Polytechnique Montréal, Safran.
[4] Consortium CIROQUO « Consortium Industriel de Recherche en Optimisation et QUantification d'incertitudes pour les données Onéreuses » en cours de montage par l’École centrale Lyon et IFPEN, suite de la chaire OQUAIDO pilotée par l’École des mines de Saint- Étienne (2016-2020).
[5] Projet « Variables de catégorie en optimisation de boîtes noires » piloté par S. Le Digabel (GERAD) et M. Munoz Zuniga (IFPEN) (2020-2021) et financé par le programme Samuel-De Champlain du fonds de recherche Nature et Technologies du Québec.
Contacts scientifiques : Delphine Sinoquet - Miguel Munoz Zuniga








