La simulation en géosciences : un exemple d’outil au service de l’environnement, des énergies et du climat

IFPEN a développé FraC [1, 2], un outil de représentation fine (maillage) d’un réseau de fractures, afin d’obtenir des simulations de référence pour le transport ou les écoulements transitoires dans les milieux géologiques.

En géoscience, simuler numériquement les processus de transport de masse ou de chaleur dans le sous-sol est essentiel. Cela est bien sûr nécessaire dans le contexte de l’exploitation pétrolière, mais aussi pour l’étude de la contamination des sols [3]. Il est ainsi classique d’injecter des traceurs (concentration d’un produit que l’on peut suivre depuis la surface) afin de mieux comprendre les interactions fluide/roche. Mais ce besoin de simulation se rencontre également en géothermie ou lors d’études de sûreté pour des stockages géologiques (chaleur, CO₂, radioéléments). Cela impose de résoudre l’équation de transport réactif ADE (Advection-Dispersion Equation), en incluant potentiellement des processus géochimiques (adsorption, désorption, dissolution, etc.).

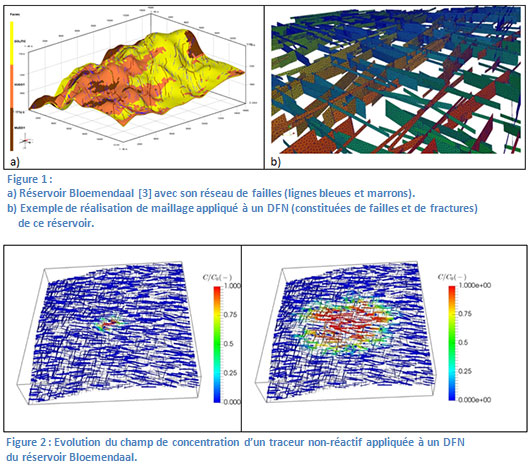
La simulation du transport devant s’appuyer sur une représentation la plus précise possible du sous-sol, elle fait l’objet d’une recherche intensive depuis de longues années. Lorsque le sous-sol présente des réseaux de fractures (DFN*), les difficultés de modélisation sont exacerbées par la complexité géométrique de ceux-ci (figure 1a,b) et par les contrastes d’écoulement pouvant exister au sein du DFN ou entre le DFN et la roche non fracturée. Pour pallier ces difficultés, il est courant de faire des approximations géométriques et d’utiliser des maillages volumiques pixélisés, associés à des propriétés physiques calculées, de manière à représenter les hétérogénéités du milieu [4] ou à obtenir des maillages optimisés en nombre de mailles [5, 6].

Si ces approximations sont acceptables en régime de diffusion pure, il peut en être autrement lorsque l’on aborde les équations de transport de type ADE à la résolution plus délicate. On dispose alors de très peu de solutions obtenues sans approximation. Celles-ci sont cependant nécessaires pour établir la plage de validité des solutions approchées, classiquement utilisées dans les outils logiciels.

C’est dans ce contexte, et au travers d’un séjour postdoctoral, que des travaux ont été initiés [1] sur un principe consistant à accepter l’augmentation du temps de simulation au profit d’une représentation fine du sous-sol. Pour cela, il a fallu développer un outil permettant de créer la représentation du réseau de fractures le plus fidèle possible (figure 1b). Le maillage obtenu possède en outre la qualité de ne pas rajouter d’hypothèses au niveau des intersections entre les fractures (maillage conforme [2]). De plus, en associant ce maillage à des outils open source ou en libre accès, comme DUMUX (université de Stuttgart) ou CAST3M (CEA), il a été possible d’obtenir des simulations de référence de l’ADE (figure 2) pour des géométries complexes de DFN, sans avoir à adapter les codes sources de ces logiciels. Ces résultats, déjà présentés dans le cadre de conférences internationales, feront bientôt l’objet d’une nouvelle publication, actuellement en cours de revue [2].

* pour "Discrete Fracture Network"

Contact scientifique : andre.fourno@ifpen.fr

Publications

1. T.-D. Ngo, A. Fourno, B. Noetinger. Modeling of transport processes through large-scale discrete fracture networks using conforming meshes and open-source soft-ware. Journal of Hydrology. Vol. 554, pp 6679. 
   >> DOI: 10.1016/j.jhydrol.2017.08.052 (2017).
      
2. A. Fourno, T.-D. Ngo, B. Noetinger. FraC : A user-friendly conforming mesh method for discrete fracture networks. 
   Submitted in J. Comp. Phys (2018).
      
3. M. Verscheure, A. Fourno, J.P. Chilès. Joint inversion of fracture model properties for CO2 storage monitoring or oil recovery history matching. Oil Gas Sci. Technol. - Revue d’IFP Energies nouvelles 67 (2), 221–235 (2012).
   >> https://ogst.ifpenergiesnouvelles.fr/articles/ogst/abs/2012/02/ogst110093/ogst110093.html
      
4. A. Fourno, C. Grenier, A. Benabderrahmane, F. Delay. A continuum voxel approach to model flow in 3D fault networks : a new way to obtain up-scaled hydraulic conductivity tensors of grid cells. Journal of Hydrology. Vol. 493, pp 68-80. 
   >> DOI: 10.1016/j.jhydrol.2013.04.010 (2013)
      
5. N. Khvoenkova, M. Delorme. An optimal method to model transient flows in 3D discrete fracture network. Peer-reviewed IAMG 2011 publication.
   >> DOI:10.5242/iamg.2011.0088 (2011)
        
6. B. Noetinger. A quasi steady state method for solving transient Darcy flow in complex 3D fractured networks accounting for matrix to fracture flow. Journal of Computational Physics, vol 283:205-223 (2015).
   >> https://www.sciencedirect.com/science/article/pii/S0021999114008006