La conception de matériaux poreux performants est un enjeu majeur pour l’efficience énergétique des procédés industriels : en catalyse, biocatalyse ou encore pour les opérations de séparation et de purification. Pour de telles applications, ces matériaux tirent leurs propriétés d’intérêt de leur microstructure particulière, comportant une grande quantité d’espaces vides organisés et connectés à l’échelle du nanomètre. IFPEN et Saint Gobain Research Provence (SGRP) se sont associés afin de se doter d’un outil facilitant à terme la mise au point de matériaux poreux optimisés en fonction d’usages donnés1 . Ils ont pour cela adopté une approche innovante par des jumeaux numériques, élaborés à partir de modèles de microstructures aléatoires et ajustés par des modèles numériques qui imitent des procédures expérimentales. Cette approche a ensuite été validée par comparaison avec des résultats d’essais sur des microstructures modèles.
La simulation numérique des aspects expérimentaux s’exerce sur des microstructures tridimensionnelles elles-mêmes simulées [1] et repose sur une approche géométrique. Ainsi, la démarche adoptée utilise essentiellement des corrélations entre des paramètres morphologiques et des quantités physiques qui caractérisent le système considéré. C’est ce passage d’une description d'états quasi-statiques de mécanismes physico-chimiques - tels que des changements de phases à l'équilibre - à celle, purement géométrique et morphologique, des phénomènes à l’œuvre qui constitue la principale difficulté à surmonter.
La morphologie mathématique, discipline scientifique qui s'intéresse depuis longtemps à la caractérisation des propriétés texturales 2D et 3D des microstructures, s’est avérée particulièrement adaptée à la résolution de ce challenge. Pour construire le matériau numérique, des algorithmes spécifiques d'extraction des réseaux de pores [2] ont tout d’abord permis de considérer des pores aux géométries complexes et arbitraires, proches de celles rencontrées dans les matériaux réels (figure). Les opérateurs de morphologie mathématique2 ont ensuite permis de simuler les phénomènes impliqués dans les techniques expérimentales de porosimétrie. Ils ont notamment permis d’estimer un opérateur d’intérêt pour ces réseaux poreux : la tortuosité (figure), propriété intimement liée aux phénomènes diffusifs puisqu’elle caractérise la facilité à traverser ces réseaux [3].
Avec ce type d’approche par jumeau numérique, les simulations d’expérimentations peuvent prendre en compte de grands volumes représentatifs, avec des arrangements multi-échelles de microstructures, et moyennant un temps de calcul raisonnable.
Pour aller plus loin encore dans l'optimisation du temps de calcul sans perte de précision sur les résultats, l’apprentissage profond est un outil prometteur en cours d’évaluation pour établir un lien direct entre des microstructures numérisées et des résultats d’essai simulés.
Cliquer sur l'animation pour l'agrandir
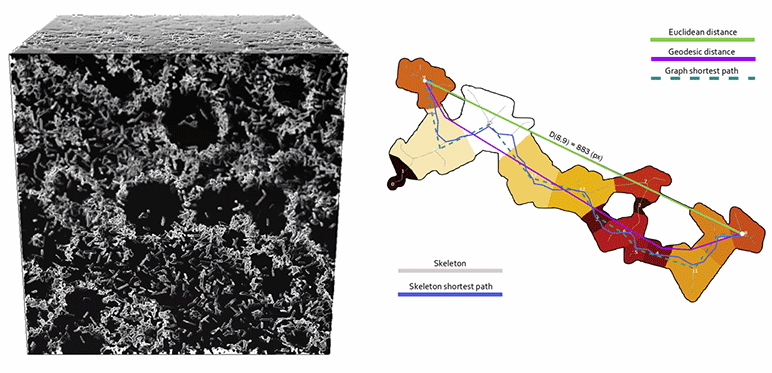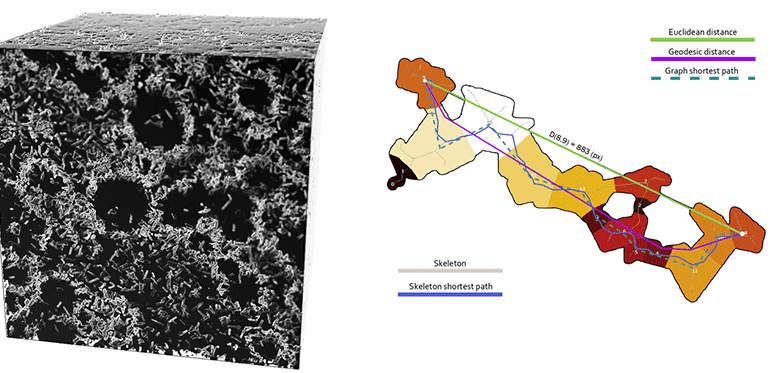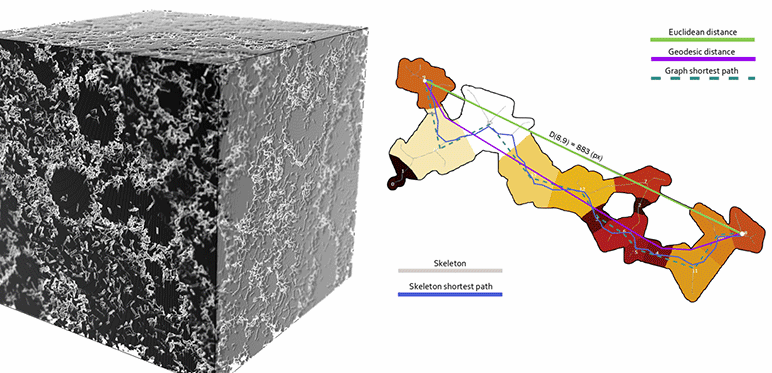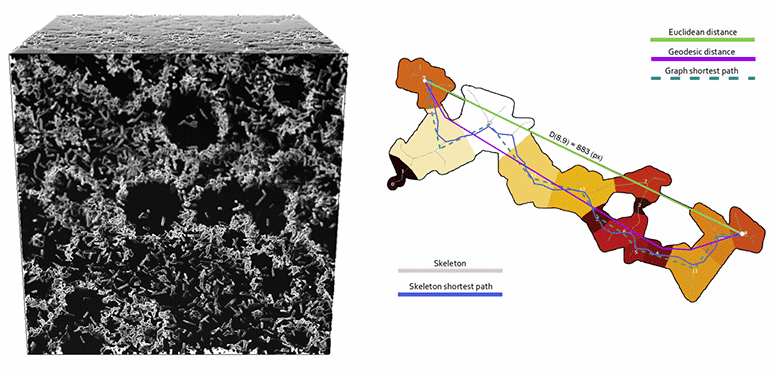
À droite, illustration d’un opérateur de tortuosité, rapport des longueurs des chemins entre deux points par « vol d’oiseau » (distance Euclidienne) et contrainte par le réseau poreux (distance géodésique).
1- Ces travaux, débutés en 2019, ont fait l’objet du travail postdoctoral d’Alexey Novikov et de la thèse de doctorat en cours d’Adam Hammoumi.
2- Voir des exemples sur https://fr.wikipedia.org/wiki/Morphologie_math%C3%A9matique
Publications :
[1] M. Moreaud, J. Chaniot, T. Fournel, J.M. Becker, L. Sorbier. Multi-scale stochastic morphological models for 3D complex microstructures. 17th Workshop on Information Optics (WIO), IEEE Conference (2018).
>> https://doi.org/10.1109/WIO.2018.8643455
[2] A. Hammoumi, M. Moreaud, E. Jolimaitre, T. Chevalier, A. Novikov, M. Klotz. Efficient Pore Network Extraction Method Based on the Distance Transform. International Conference on Artificial Intelligence & Industrial Applications. Springer Ed. (2020).
>> https://doi.org/10.1007/978-3-030-53970-2_1
[3] A. Hammoumi, M. Moreaud, E. Jolimaitre, T. Chevalier, A. Novikov, M. Klotz. Graph-based M-tortuosity estimation. IAPR International Conference on Discrete Geometry and Mathematical Morphology (2021).
Contact scientifique : Maxime Moreaud






