L’hypothèse d’un mouvement de particule elliptique des modes propres des onde-S de volume projetés sur un supposé plan commun de polarisation elliptique de l'un quelconque des vecteurs d'ondes S propres S1, S2 associés à un vecteur d'onde donné K a été développé dans un précédent travail académique sur l'anisotropie des ondes élastiques de cisaillement (Elastic shear wave anisotropy [1], Eudier, 1988).
Cette étude avait été initiée en 1988 par Naville, pour tenter de définir les formes théoriques relatives des mouvements de particule des modes propres d'onde de cisaillement en transmission, dans le but de simplifier la détection des paramètres d'anisotropie d’onde-S par le traitement spécifique des signaux de sismique de surface et de sismique de puits (VSP). Les signaux sismiques à trois composantes mesurés constituent les déplacements, vitesses ou accélérations OBSERVABLES décrits dans la théorie de l'élasticité.
Les résultats obtenus en 1988 sont intéressants, mais n'ont pas été pleinement interprétés à l'époque. En effet, en raison de la symétrie du tenseur des contraintes complexes (L. Landau & E. Lifchitz [2]) le produit de convolution simple des vecteurs de déplacement du mouvement des particules propres est nul : tS1*S2 = 0. Noter que le produit simple est différent du produit scalaire hermitien. Cette propriété conduit à l'observation attendue d’un mouvement elliptique des particules parcouru dans le MÊME sens de rotation pour les deux modes propres d'onde S se propageant dans la même direction spatiale.
En pratique, l’ellipticité du mouvement des particules sismiques n'est pas observée de manière spatialement cohérente sur les ondes P directes uniques et les ondes S directes enregistrées par les outils modernes de VSP de haute qualité caractérisés par leur excellent couplage mécanique à la paroi de puits, assurant ainsi leur isotropie de réponse en réception, appelée ”fidélité vectorielle”.
Dans l'addendum à l'étude d'Eudier, Naville explicite une manière de changer le système de coordonnées d'axes linéaires du plan de polarisation de cisaillement 2D en un système de coordonnées vectorielles elliptiques dans le but de faciliter le processus informatique de détection de l'anisotropie des ondes S. Cependant, des questions subsistaient sur la signification physique des paramètres supplémentaires apportés par l'observation éventuelle de modes d'onde S propres elliptiques et sur ce qu'il advient de la forme des ondes S propres lorsque plusieurs réseaux de fractures sont présents dans un échantillon de roche. De plus, une singularité se produit lorsque l'ellipticité augmente au point que les deux modes propres deviennent circulaires en tournant dans le même sens de rotation, si bien qu’ils fusionnent ! Enfin, il est notoire que la présence éventuelle de S-modes propres elliptiques exprimerait une différence d'orientation des directions propres linéaires de la partie réelle symétrique du tenseur de rigidité par rapport à la partie imaginaire symétrique du même tenseur complexe, et cette différence serait difficile à expliquer physiquement.
Vers 2010, après avoir analysé de nombreux jeux de données VSP de terrain et après réflexion, l'auteur suggère définitivement que la rotation angulaire identique des ondes S représente une idée irréaliste et aberrante, non soutenue par les observations. Par conséquent, les formes des mouvements de particules des modes d’onde propre S1 et S2 projetées sur un plan de polarisation initialement supposé elliptique de S1, dégénèrent toutes deux en mouvements linéaires orthogonaux, dans le plan orthogonal au vecteur d'onde K dans un milieu de propagation viscoélastique anisotrope homogène ; ce phénomène est appelé « biréfringence ordinaire » par L. Landau & E. Lifchitz [2].
Un argument supplémentaire fait référence à la forme d'une onde S elliptique incidente après réflexion en incidence normale sur un plan réflecteur parfaitement isotrope, c'est-à-dire un réflecteur total avec un coefficient de réflexion égal à l'unité (miroir parfait). Dans le fichier joint intitulé : Réflexion de l'onde de cisaillement elliptique (Elliptical Shear wave reflection [3]), l'onde S elliptique réfléchie conserve le même mouvement de forme elliptique (réponse temporelle du signal) avec la même rotation angulaire que celle du signal incident, tout en se propageant dans la direction opposée. En conséquence, dans un milieu anisotrope, un réflecteur total isotrope orthogonal à la direction de vitesse de groupe (ou rayon portant l’énergie) de l'onde S incidente inverse la propagation de l'onde S le long du même rayon incident, même si cette direction de rayon en milieu anisotrope s'écarte légèrement de la normale au plan de polarisation de l'onde S elliptique. La normale au plan de polarisation de l’onde-S réfléchie est symétrique de la normale au plan de polarisation de l’onde-S incidente.
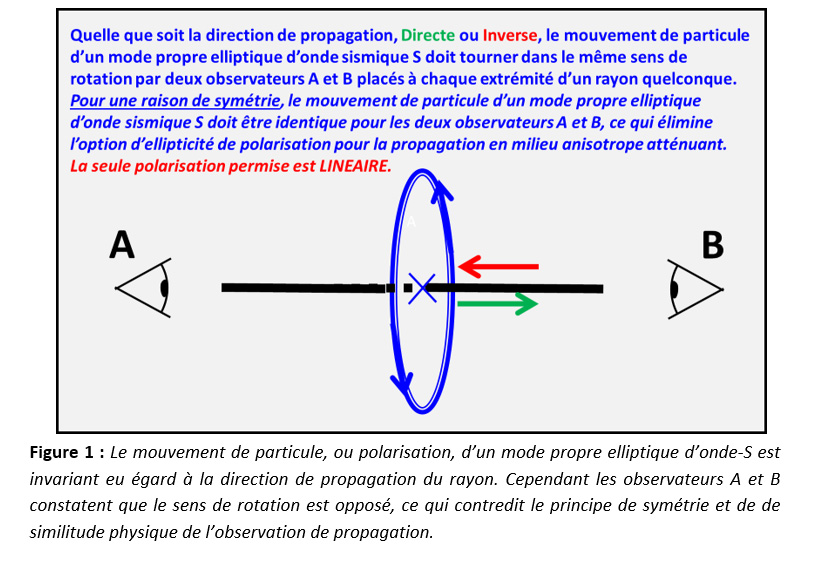
L'identité de la rotation angulaire d'un mouvement elliptique supposé d'un mode propre d’onde S pour la propagation aller-retour le long du même trajet de rayon donné s'avère irréaliste car elle viole le principe de symétrie de propagation, comme illustré sur la figure 1. Pour respecter ce principe, la seule polarisation permise en milieu anisotrope homogène atténuant (ou anélastique) pour les modes propres sismiques est la polarisation linéaire.
Conclusions
Dans un milieu homogène anisotrope et viscoélastique, et pour tout trajet spatial le long d’un rayon ou du vecteur de groupe, les mouvements de particule des modes propres d’onde de volume P et S sont linéaires ; ils ne sont peut-être pas toujours mutuellement orthogonaux, déviant d'un petit angle, mais ils restent polarisés linéairement.
Bien que la direction de polarisation d'onde P puisse ne pas coïncider avec la direction du vecteur de propagation/vitesse de phase K dans un milieu anisotrope, elle peut également s'écarter de quelques degrés de la direction du vecteur vitesse de groupe, ou du rayon (réf : S. Crampin [4], 1982, figure 1).
Par conséquent, les directions linéaires de vecteur propre du tenseur des contraintes coïncident spatialement avec les directions linéaires de vecteur propre du tenseur d’atténuation/dissipation.
La polarisation linéaire des ondes P est couramment observée sur les données de VSP à 3 composantes enregistrées sur de grands volumes de formations rocheuses homogènes et atténuantes forées par de nombreux puits dans le monde. Les observations de la polarisation linéaire propre des ondes P et S ultrasonores sont également largement rapportées, présentant souvent deux ondes S principales avec des vitesses et des atténuations notablement différentes dans des carottes anisotropes homogènes.
Par chance, la polarisation linéaire des ondes de sismiques de volume observée dans toutes les études expérimentales et les mesures industrielles sur une très large gamme de fréquences, depuis les basses fréquences sismologiques et sismiques jusqu’aux hautes fréquences ultrasonores, permet d'affiner les détails théoriques de la propagation et de la biréfringence des ondes S dans les zones viscoélastiques homogènes de la subsurface terrestre.
La polarisation elliptique des ondes inhomogènes de volume en transmission, décrites par R.D. Bordcherdt-73 [5] et R.D. Bordcherdt-86 [6] n’est pas mise en évidence par les observations industrielles. Cette ellipticité hypothétique serait-elle trop petite pour être identifiée de façon consistante sur les longs intervalles-profondeur de propagation des mesures VSP (Profil Sismique Vertical) ? Les instruments modernes de la technique de VSP ont grandement contribué à la précision des observations de propagation des ondes sismiques.
En conséquence, la polarisation linéaire des modes propres d’ondes transmises en milieu homogène anisotrope en vitesse et anisotrope en atténuation est la seule retenue dans l’interprétation des observations par les divers utilisateurs dans l’exploration du sous-sol.
|
Contact scientifique : |
Références :
- Elastic shear wave anisotropy / F. Eudier (ENS - Ecole Normale Supérieure de Lyon) - Anisotropie des ondes de cisaillement élastiques L'Anisotropie et les Phénomènes d'Atténuation. Effets sur les ondes ultrasonores. Application à la Prospection Pétrolière (Addenda en anglais)
>> Rapport de stage de Diplôme d'Etudes Approfondies d'Acoustique physique (DEA), Paris, 1988.
- L. Landau & E. Lifchitz / Théorie de l’élasticité, Editions Mir, 1967.
>> https://archive.org/details/landau-lifchitz-physique-theorique-vol-07-theorie-de-lelasticite-mir-1967
- Elliptical Shear wave reflection / C. Naville (IFPEN) - Réflexion d'onde de cisaillement elliptique. Mode propre elliptique d'onde de cisaillement après réflexion en incidence normale sur une interface isotrope, propagée dans un milieu homogène.
>> Note 2022.
- S. Crampin / Stuart Crampin, Ralph A. Stephen, Robert McGonigle - The polarization of P-waves in anisotropic media, Geophysical Journal International, Volume 68, Issue 2, February 1982, Pages 477–485
>> https://doi.org/10.1111/j.1365-246X.1982.tb04910.x
- R.D. Borcherdt-73 / Energy and plane waves in linear viscoelastic media, Journal Geophysical Research, 78, (N°14), 2442-2456.
>> https://doi.org/10.1029/JB078i014p02442
- R.D. Borcherdt-86 / Borcherdt,R.D., G. Glassmoyer, L. Wennerberg, 1986: Influence of welded boundaries in anelastic media on energy flow, and characteristics of P, S-I, and S-II waves: Observational evidence for inhomogeneous body waves in low-loss solids, Journal Geophysical Research, 91, 11,503-11,518
>> https://doi.org/10.1029/JB091iB11p11503






