Le calcul des écoulements d’eau et de gaz dans les milieux rocheux complexes et hétérogènes est au cœur des solutions technologiques en lien avec les enjeux climatiques et énergétiques actuels, comme par exemple le stockage souterrain de CO2 ou de chaleur. Pour ce type de calculs, un modèle adaptatif a été développé par les chercheurs d’IFPEN et de PoliMi1 afin de mieux prendre en compte la nature très discontinue du sous-sol. La collaboration entre les deux instituts se poursuit pour améliorer la performance de ces simulations numériques.
1 Université polytechnique de Milan
Des distributions spatiales irrégulières de porosité et de perméabilité
Simuler numériquement l’écoulement d’eau et de gaz dans un milieu poreux hétérogène revêt une grande importance pour certaines applications nouvelles, en lien avec les enjeux climat/énergie, comme le stockage dans le sous-sol de CO2 ou de chaleur. Les hétérogénéités du milieu en question relèvent à la fois de la diversité dans la nature des roches mais aussi de la présence de structures géométriques complexes, comme des chenaux ou des macropores : elles se traduisent par des distributions spatiales irrégulières de porosité et de perméabilité telles qu’illustrées par les exemples de la figure 1.
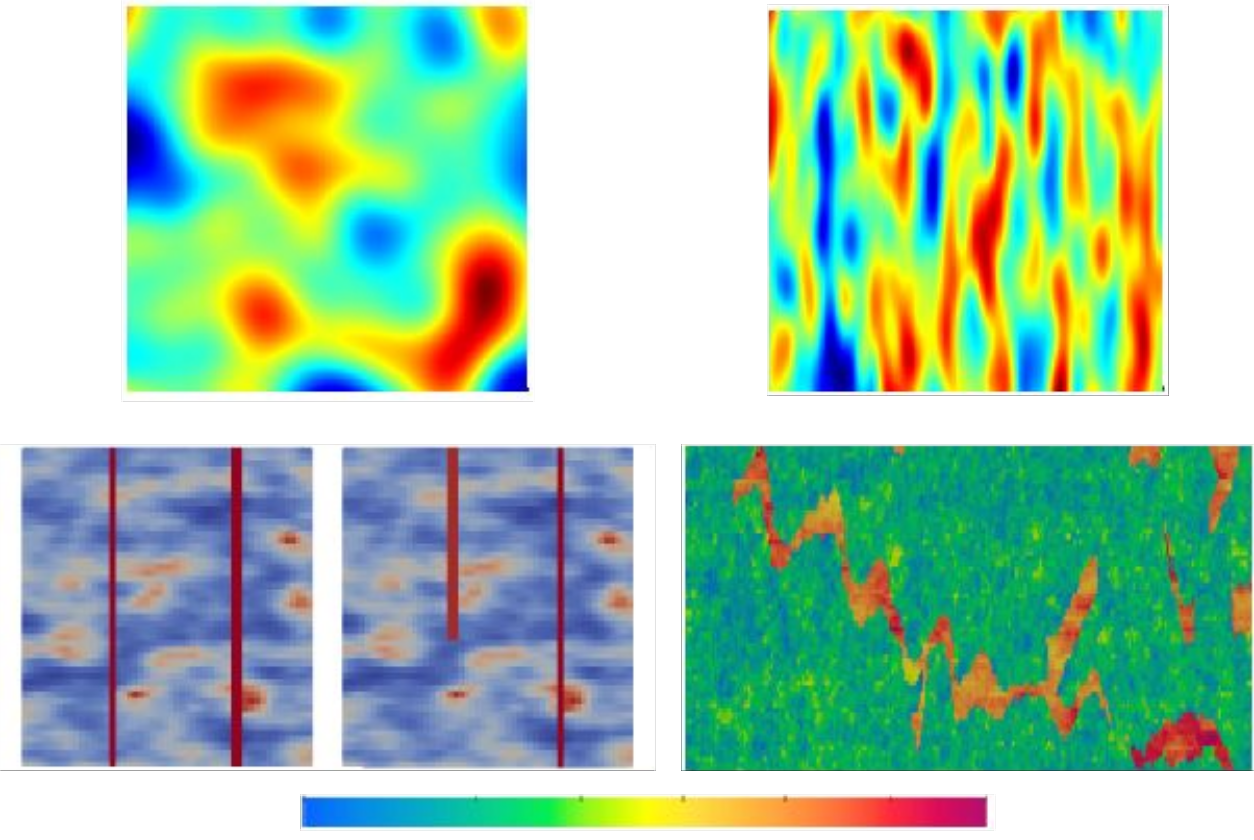
En haut à gauche : généré par une distribution gaussienne isotrope [3]
En haut à droite : généré par une distribution gaussienne anisotrope [3]
En bas à gauche : générés par une distribution de Matérn [3,4] avec macropores transverses [4] représentés par des traits rouges verticaux
En bas à droite : mesuré sur la couche 35 du projet SPE10 [5]
La loi de Darcy et ses limites
En termes de modélisation, le choix de la loi constitutive qui relie la vitesse d'écoulement des fluides au gradient de pression est essentiel. Il est classique d'utiliser la loi de Darcy sur la totalité du domaine concerné par la simulation : elle est linéaire, donc peu coûteuse numériquement, et décrit bien les écoulements à faibles vitesses. Lorsque ces vitesses s'élèvent, par exemple dans les structures très perméables, la linéarité n’est plus respectée et la loi de Darcy perd de sa pertinence. Ainsi, il a été montré expérimentalement qu’elle conduit à surestimer les grandes vitesses calculées [6,7]. Afin de corriger cet effet, il est courant d'ajouter un terme quadratique à la loi de Darcy et ainsi de la transformer en loi de Forchheimer. Ce terme additionnel agit par une prise en compte des effets inertiels en augmentant l’énergie d’écoulement. Toutefois, à cause de la non-linéarité ainsi introduite, la résolution des équations spatialement discrétisées se révèle coûteuse en temps de calcul.
Adoption d’un modèle adaptatif
Pour remédier à cet effet en impactant le moins possible la précision des résultats, des chercheurs d'IFPEN et de PoliMi ont proposé un modèle adaptatif [1,2] qui n’emploie qu’à bon escient la loi de Forchheimer. Ainsi, pour la résolution numérique en tout point du domaine, le choix de la loi qui s’applique est effectué, à chaque itération, selon un critère fondé sur des grandeurs physiques (telles que la perméabilité du domaine et la viscosité des fluides) et qui porte sur la vitesse d’écoulement : si celle-ci excède la valeur du critère, la loi de Forchheimer est utilisée.
Régularisation du problème adaptatif
Une difficulté majeure de ce modèle adaptatif réside dans les discontinuités que crée le passage abrupt d'une loi constitutive à l'autre dans les zones dites de transition. En effet, ces discontinuités ont une répercussion forte sur la formulation mathématique du modèle et le rendent difficile à manipuler. Pour pallier cette difficulté, IFPEN et PoliMi ont proposé une régularisation du problème adaptatif fondée sur un moyennage des vitesses dans les zones de transition. Le passage d'une loi à l'autre s’en trouve lissé, effaçant ainsi la discontinuité préjudiciable. Outre l'existence et l'unicité des solutions pour les deux approches (problèmes « discontinu » et « régularisé ») on a vérifié qu’elles convergeaient bien vers la même [1,2]. La figure 2 montre le partitionnement du domaine pour le projet SPE10 de la figure 1 dans le cas du modèle régularisé, pour trois valeurs distinctes du critère de vitesse : plus le critère est bas et plus les régions où l’équation de Forchheimer s’applique sont étendues.

De la gauche vers la droite : critère de vitesse décroissant
Des efforts encore nécessaires pour mieux prédire les sous-régions de calcul
Bien que le modèle régularisé soit continu, il n'en reste pas moins fortement non linéaire dans les zones de transition ; il peut donc demeurer coûteux à utiliser numériquement. Une collaboration en cours s’attache à diminuer encore le temps de calcul, en employant le modèle régularisé comme prédicteur des régions « Darcy » et « Forchheimer », de sorte que la simulation numérique fasse directement appel à la loi prédite dans chaque région, sans zones de transition. Ainsi, à la fois la discontinuité du modèle adaptatif et l'excès de non-linéarité du modèle régularisé seront éliminés. L'étape de prédiction fera appel à des techniques d'apprentissage automatique, en faisant des hypothèses préalables sur le domaine de la simulation : géométrie des régions constitutives, conditions aux limites en pression et en vitesse comme données d’entrée du modèle.
Références:
1. FUMAGALLI, A., PATACCHINI, F. S. (2022). Model adaptation for non-linear elliptic equations in mixed form: existence of solutions and numerical strategies. ESAIM: Mathematical Modelling and Numerical Analysis, 56(2), 565–592. DOI : https://doi.org/10.1051/m2an/2022016.
2. FUMAGALLI, A., PATACCHINI, F. S. (2022). Well-posedness and variational numerical scheme for an adaptive model in highly heterogeneous porous media. ArXiv 2206.07970. Lien arXiv : https://arxiv.org/abs/2206.07970.
3. PICHOT, G., LEGRAND, S., KERN, M., TEPAKBONG-TEMATIO, N. (2022). How to initialize the Circulant Embedding method to speed up the generation of stationary Gaussian Random Fields? HAL 03190252. Lien HAL : https://hal.inria.fr/hal-03190252.
4. WINTER, R., VALSAMIDOU, A., CLASS, H., FLEMISCH, B. (2022). A study on Darcy versus Forchheimer models for flow through heterogeneous landfills including macropores. Water, 14(4), 546. DOI : https://doi.org/10.3390/w14040546.
5. CHRISTIE M. A., BLUNT. M. J. (2001) Tenth SPE Comparative Solution Project: A Comparison of Upscaling Techniques. Society of Petroleum Engineers, Houston, Texas. DOI : https://doi.org/10.2118/66599-MS.
6. ZHANG, T., ZHAO, Y., GAN, Q., YUAN, L., ZHU, G., CAI, Y., CAO, B. (2018). Experimental investigation of Forchheimer coefficients for non-Darcy flow in conglomerate-confined aquifer. Geofluids, 1–21. DOI : https://doi.org/10.1155/2018/4209197.
7. SOBIESKI, W., TRYKOZKO, A. (2014). Darcy’s and Forchheimer’s laws in practice. Part 1. The experiment. Technical Sciences, 17(4), 321–335. Lien web : https://www.infona.pl/resource/bwmeta1.element.baztech-2757664d-c0fc-43c9-9c80-dc3a5f6572e9.
Contact scientifique : Francesco Patacchini






