Facebook Twitter LinkedIn Imprimer

Les lignes d’ancrage, le plus souvent constituées de câbles en acier au carbone, sont des éléments essentiels pour la stabilité de structures flottantes en mer, comme celles supportant des éoliennes. Pour pallier le risque de rupture en service, des lignes redondantes sont généralement prévues à la conception, ce qui entraîne un surcoût notable. L’enjeu est d’améliorer la fiabilité des câbles pour limiter ces redondances, par une meilleure prédiction de leur durée de vie en fatigue.

La fatigue des câbles acier est un phénomène multi-échelle. Il dépend à grande échelle des variations de tension et de courbure liées aux sollicitations par le vent, les vagues et les courants. A l’échelle métrique, le comportement dépend des frottements entre les fils constituant les câbles (Figure 1). Enfin, à l’échelle millimétrique du contact entre fils, le phénomène dépend du chargement mécanique local et de l’environnement (air, eau de mer, graisse).

La démarche suivie à IFPEN, en collaboration avec le laboratoire LMPSa de l’Ecole Normale Supérieure et le laboratoire LTDSb de l’Ecole Centrale Lyon, a consisté à remplacer une prédiction actuellement empirique de la tenue en fatigue par une modélisation multi-échelle fondée sur la physique. A l’échelle macroscopique, les zones critiques de la ligne d’ancrage sont déterminées avec une simulation aéro-servo-hydro-élastiquec de la structure flottante qui tient compte du chargement en vent, vagues et courant marin. On en déduit un chargement, en tension et courbure variables, d’un modèle FEMd mésoscopique (dizaine de mètres) du câble qui prédit le glissement et l’état de contraintes entre les fils (Figure 2). A l’échelle du contact entre les fils, la modélisation permet de vérifier le respect d’un critère de fretting-fatiguee identifié expérimentalement en tenant compte de l’environnement (Figure 3) et qui correspond à la transition glissement partiel/ glissement totalf .

Les travaux menés ont conduit à des progrès significatifs pour la simulation du comportement des lignes d’ancrage en acier et à une meilleure compréhension du comportement en fretting-fatigue des fils qui les constituent.

Sur le premier aspect, à l’échelle mésoscopique, le nouveau modèle FEM permet d’abaisser considérablement le temps de calcul. Des travaux en cours cherchent à poursuivre cette diminution grâce à une réduction de modèle par la méthode PGD-LATIN [3] du LMPS.

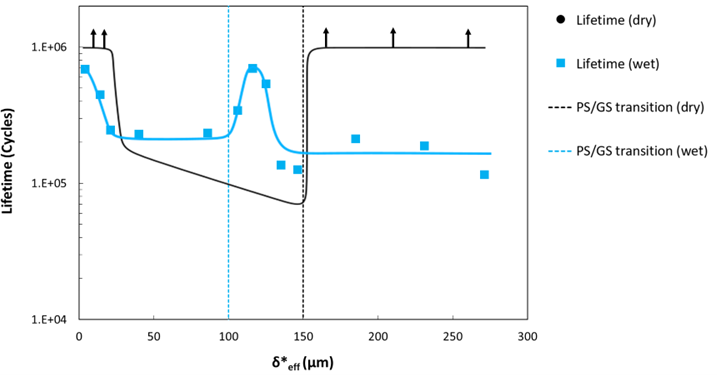
Sur le second aspect, en plus de mettre en évidence l’existence d’un glissement critique, les essais de fretting-fatigue ont montré l’influence déterminante mais complexe et parfois contre-intuitive du milieu environnant. La graisse a un effet positif mais limité, car elle a du mal à entrer dans le contact. L’eau de mer a deux effets antagonistes : d’un côté elle réduit l’endommagement par son pouvoir lubrifiant, de l’autre elle l’augmente par son action corrosive. Selon le chargement, l’un ou l’autre mécanisme l’emporte (figure 4). Les essais en eau de mer ont été faits dans une cellule aérée, avec contrôle du potentiel électrochimique.
    

Fig. 1 : section d’un câble d’ancrage acier
Figure 1 : section d’un câble d’ancrage acier


 

Fig. 2 : Modèle éléments finis d’un câble avec contact et frottement [1].
Figure 2 : Modèle éléments finis d’un câble avec contact et frottement  [1].

 

Figure 3 : Essai de fretting-fatigue sur un fil de câble au LTDS [2]
Figure 3 : Essai de fretting-fatigue sur un fil de câble au LTDS [2]

 

Figure 4
Figure 4 : courbe de fretting-fatigue (glissement en abscisse, cycles à rupture en ordonnée) pour le contact acier-acier sec (noir) et en eau de mer (bleu). PS/GS : « partial slip / gross slip »


a- Laboratoire de Mécanique Paris-Saclay
b- Laboratoire de Tribologie et Dynamique des Systèmes
c- Aérodynamique + servo pour le contrôleur + hydrodynamique pour les corps immergés + élastique pour la structure.
d- Modèle éléments finis : de type poutres en contact avec frottement en rotations finies et petits déplacements
e- Fissure amorcée en fretting puis propagée en fatigue
f- Glissement partiel : une partie de la surface de contact glisse, l’autre reste collée ; glissement total : toute la surface de contact glisse
  

Références :

  1. F. Bussolati, M. Guiton, P.-A. Guidault, O. Allix, and P. Wriggers: Lecture Notes in Application and Computational Mechanics, vol. 93 (2019). 
       
  2. S. Montalvo, S. Fouvry, M. Martinez, F. Ropital, Tribology International, two articles submitted
      
  3. A. Nouy and P. Ladeveze. Multiscale Computational Strategy with Time and Space Homogenization: A Radial-Type Approximation Technique for Solving Microproblems, International Journal for Multiscale Computational Engineering, 2(4), (2004).
    >> DOI: 10.1615/IntJMultCompEng.v2.i4.40 
      

Contacts scientifiques : martin.guiton@ifpen.fr ; michael.martinez@ifpen.fr ; francois.ropital@ifpen.fr

>> NUMÉRO 49 DE SCIENCE@IFPEN