La simulation des écoulements dans le sous-sol fait intervenir des mélanges polyphasiques complexes dans lesquels des phases peuvent apparaître et disparaître au cours du temps. Pour gérer cette complexité, plusieurs approches ont été testées (formulation unifiée, méthode de points intérieurs non-paramétrique, etc.) au cours d’un travail de thèse. La nouvelle méthode mise en place est très robuste et permet d’obtenir ainsi une bonne convergence des algorithmes de résolution.
Gestion des phases d’un mélange
Dans de nombreux simulateurs du sous-sol (stockage du CO2, géothermie, réservoir), une partie délicate concerne les mélanges polyphasiques et plus particulièrement la prise en compte des lois d’équilibre thermodynamique relatives aux espèces chimiques présentes. La difficulté réside dans la gestion de l'apparition et de la disparition des phases pour différents constituants. L'approche dynamique traditionnelle, dite de variable switching, consiste à ne garder que les inconnues des phases présentes et les équations relatives à celles-ci. Elle est toutefois lourde et coûteuse, dans la mesure où cette action doit être effectuée en continu, même d'une itération à l'autre au sein d’une procédure de résolution numérique, comme par exemple l’algorithme de Newton classique.
Apport de la formulation unifiée
Une approche alternative, appelée formulation unifiée et proposée récemment par Lauser et al. [1], permet de maintenir un jeu fixe d'inconnues et d'équations tout au long des calculs. Sur le plan théorique, c'est un progrès important qui a suscité ensuite beaucoup de travaux dans la communauté du calcul scientifique. Sur le plan pratique toutefois, la nouvelle formulation fait intervenir des équations de complémentarité qui sont non-différentiables. On est alors obligé, après discrétisation, d'avoir recours à la méthode semi-lisse Newton-min, laquelle ne garantit pas la convergence vers une solution unique. Ainsi, toute la difficulté du problème se retrouve transférée à la l’étape de résolution numérique mais elle n’a pas disparu.
Élaboration d’une méthode de points intérieurs non-paramétrique
Pour ne pas s’arrêter à mi-chemin et aller au bout de l’intérêt de la démarche par formulation unifiée, une équipe de chercheurs d’IFPEN et de l’INSA de Rennes a décidé de lever ce dernier obstacle. Dans le cadre d’une thèse co-encadrée [2], ils ont visé l’élaboration d’algorithmes de résolution mieux adaptés, offrant une meilleure convergence des calculs. La démarche suivie a consisté à s’inspirer de méthodes ayant fait leur preuve en optimisation sous contraintes et à les transposer aux systèmes d’équations généraux (qui ne proviennent pas nécessairement d’un problème d’optimisation). C’est ainsi que pour les systèmes algébriques, il a été proposé une version non-paramétrique1 des méthodes de points intérieurs2 appelées NPIPM. Ces méthodes sont reconnues pour leur grande efficacité en optimisation [3].
1 « non-paramétrique » signifie qu’il n’est pas nécessaire de faire tendre vers 0 « à la main » le paramètre de régularisation qui intervient dans les méthodes de points intérieurs et qui constitue souvent leur « maillon faible ».
2 « intérieur » signifie qu’au cours des itérations, le vecteur inconnu reste à l’intérieur d’une région où les contraintes de positivité sont strictement satisfaites.
Analyse et extension des lois d’état cubiques
Une autre contribution importante de la thèse [3] a été la compréhension et la résolution partielle d’une autre obstruction au bon fonctionnement de la formulation unifiée, jusque-là non identifiée dans la littérature. Il s’agit de la limitation du domaine de définition des fonctions de Gibbs3 associées aux lois d’état cubiques4. Pour remédier à l’éventuelle non-existence de solution du système, il a été préconisé un prolongement naturel des fonctions de Gibbs. De même, un grand nombre de propriétés théoriques jusqu’alors inconnues de la formulation unifiée ont été établies [4]. La complémentarité de ces résultats avec les aspects numériques de la méthode NPIPM a été éprouvée comme décrit ci-après.
3 fonction enthalpie libre G associée au second principe de la thermodynamique.
4 équation d'état d'un fluide pouvant s'écrire sous la forme d'un polynôme de degré trois en fonction du volume.
Comparaison numérique sur plusieurs modèles d’équilibre de phases
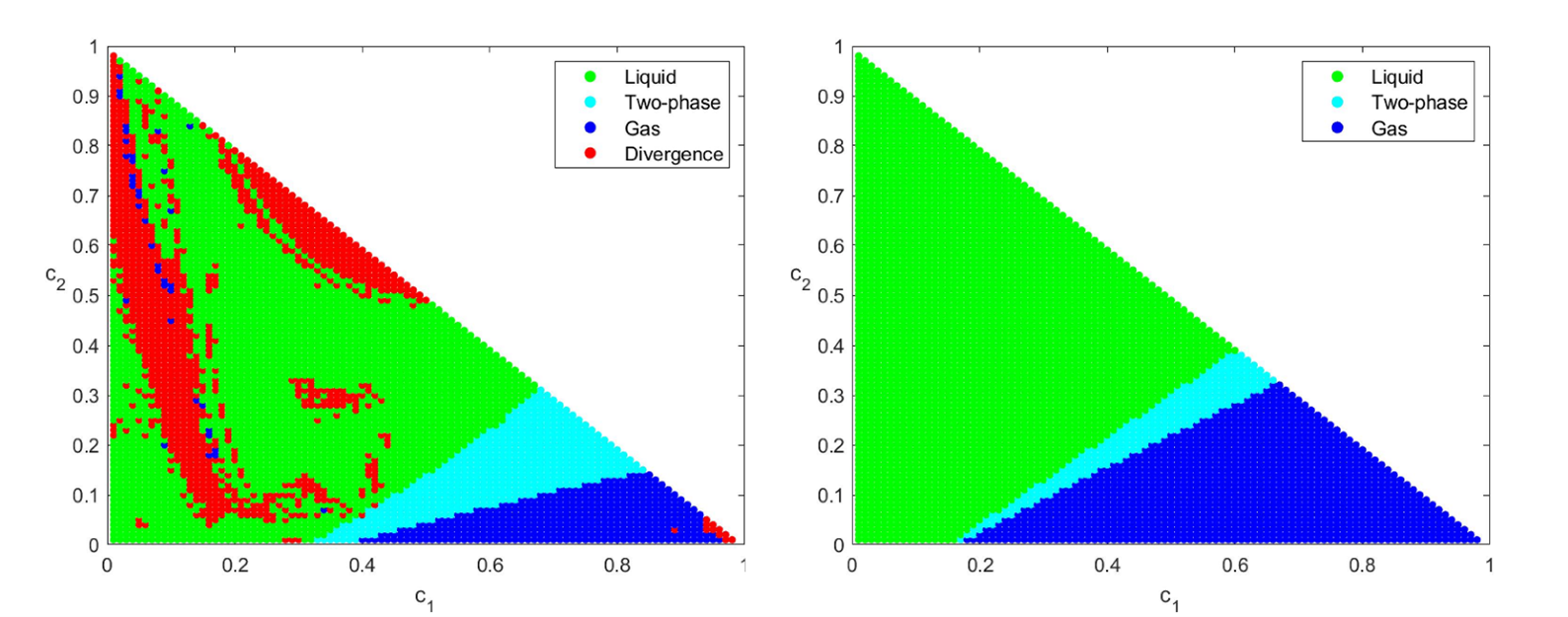
En termes de robustesse de convergence, la combinaison de la nouvelle méthode NPIPM avec l’extension des fonctions de Gibbs permet d’obtenir des résultats supérieurs à la méthode Newton-min. À titre d’exemple, la partie gauche de la figure 1 signale en rouge, dans l’espace des concentrations (c1, c2), les états pour lesquels Newton-min diverge, pour un choix donné quant au point de départ du calcul. À droite, avec le même point initial mais grâce à NPIPM, ces états problématiques ont disparu sur les différentes zones du domaine : liquide (vert), gaz (bleu), diphasique (liquide-gaz, cyan).
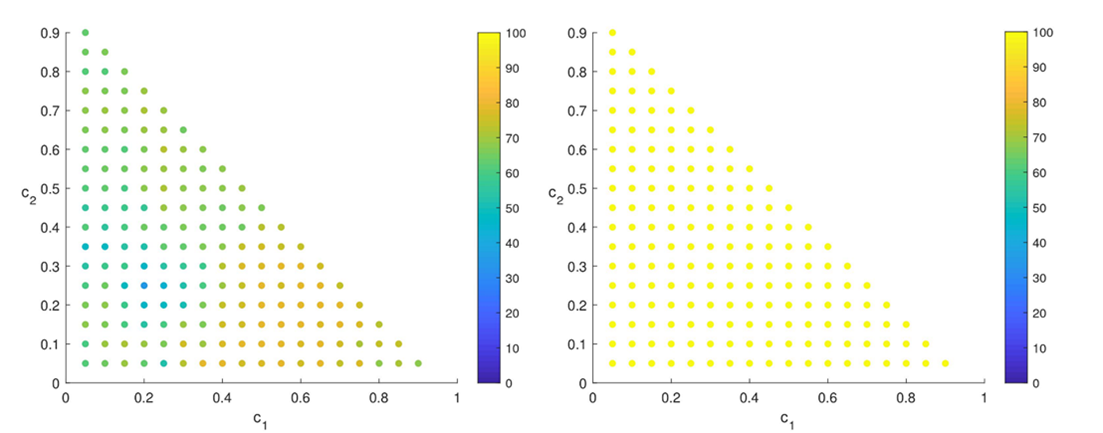
La figure 2 représente d’une autre manière le bénéfice de la nouvelle méthode : elle indique le nombre de situations (point initial) pour lesquelles chacun des deux algorithmes converge. On constate que NPIMP (droite) atteint le score de 100% sur tous les cas considérés, contrairement à Newton-min (gauche). Pour ces tests numériques, nous avons considéré la loi d’état cubique de Peng-Robinson avec des fonctions de Gibbs étendues [5].
Références:
[1] A. LAUSER, C. HAGER, R. HELMIG, B. WOHLMUTH, A new approach for phase transitions in miscible multiphase flow in porous media, Advances in Water Resources 34 (2011), pp. 957–966. https://doi.org/10.1016/j.advwatres.2011.04.021
[2] D. T. S. VU, Numerical resolution of algebraic systems with complementarity conditions. Applications to the thermodynamics of compositional multiphase mixtures, PhD thesis 2020UPASG006, Université Paris-Saclay, 2020. https://tel.archives-ouvertes.fr/tel-02987892
[3] M. H. WRIGHT, The interior-point revolution in optimization: history, recent developments, and lasting consequences, Bulletin of the American Mathematical Society 42 (2005), pp. 39–56. https://doi.org/10.1090/S0273-0979-04-01040-7
[4] I. BEN GHARBIA, M. HADDOU, Q. H. TRAN, D. T. S. VU, An analysis of the unified formulation for the equilibrium problem of compositional multiphase mixtures, ESAIM: M2AN 55 (2021), pp. 2981–3016. https://doi.org/10.1051/m2an/2021075
[5] D. T. S. VU, I. BEN GHARBIA, M. HADDOU, Q. H. TRAN, A new approach for solving nonlinear algebraic systems with complementarity conditions. Application to compositional multiphase equilibrium problem, Mathematics and Computers in Simulation 190 (2021), pp. 1243–1274. https://doi.org/10.1016/j.matcom.2021.07.015
Contacts scientifiques : Ibtihel.Ben-Gharbia@ifpen.fr, Quang Huy Tran






