L’équation de Richards, qui permet de simuler les flux d’eau dans des sols partiellement saturés, est difficile à résoudre dans des milieux fortement hétérogènes où la pression capillaire peut varier brutalement. Une nouvelle méthodologie a été mise en place pour améliorer la robustesse et la précision des calculs dans ce type de milieux. Une des applications envisagées est le stockage souterrain de CO2.
Résolution de l’équation de Richards : quels enjeux numériques ?
L’équation de Richards est un modèle d’écoulement simplifié, fréquemment utilisé en hydrogéologie pour simuler les flux d’eau dans des sols partiellement saturés. Sa résolution se fait classiquement à l’aide d’un schéma de discrétisation en espace, de type volumes-finis. Mais le système d’équations non-linéaires résultant se révèle, dans certains cas, difficile à résoudre et la précision des solutions obtenues peut être dégradée lorsque la loi de pression capillaire est spatialement hétérogène.
Des chercheurs d’IFPEN et d’Inria ont proposé dans le cadre de travaux de thèse [1] une nouvelle version de ce schéma de discrétisation, plus robuste face aux non-linéarités du problème mais aussi plus précis. Ils ont de plus établi la preuve théorique de l’existence et de l’unicité des solutions discrètes ainsi que leur convergence vers une solution du problème variationnel.
Une forte non-linéarité et une discontinuité spatiale de la pression capillaire
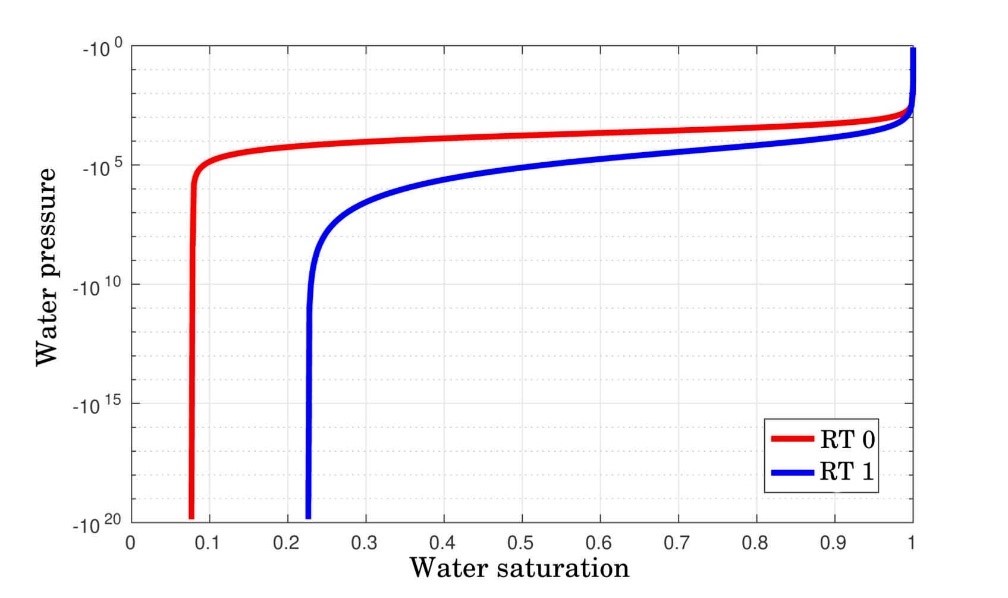
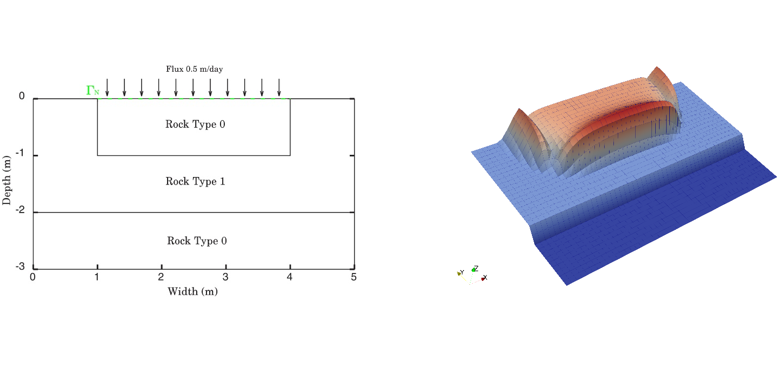
La pression capillaire est définie comme la différence de pression existant à l’interface entre deux phases, une considérée comme mouillante vis-à-vis de la roche poreuse et l’autre non. Dans la formulation de Richards, ces deux phases correspondent respectivement à l’eau et l’air. La pression de ce dernier étant supposée constante, la pression de l’eau se déduit donc directement de la pression capillaire, grandeur généralement définie sous la forme d’une fonction non linéaire de la saturation d’eau et dépendante également du type de roche localement présent (Figure 1). Cette dernière dépendance peut de plus faire apparaître des discontinuités de la saturation d’eau au cours du temps et donc des accumulations ou des succions d’eau au niveau des interfaces de changement de roche (Figure 2). Une modélisation précise de ces phénomènes est donc importante.
La technique du paramétrage : une solution pour améliorer la convergence de l’algorithme de Newton
Face à la non-linéarité de la loi décrivant la pression capillaire, l’algorithme de Newton, utilisé pour résoudre l’équation discrétisée, peut converger difficilement, voire pas du tout. Cet écueil peut en grande partie être réduit moyennant un changement de variables adapté et régulier au cours des itérations. C’est le principe de la technique de paramétrage proposée dans [2]. Ce précédent travail utilisait la transformée de Kirchhoff comme variable potentielle pour opérer l’algorithme de Newton mais celle-ci ne peut pas toujours être calculée. Le travail réalisé au cours de cette nouvelle étude a permis de proposer des paramétrages basés directement sur la saturation de l’eau et la pression capillaire, assurant ainsi une bonne convergence des calculs avec des lois pourtant très non-linéaires [3].
Un raffinement simplifié pour une précision accrue aux interfaces de changement de roche
Une discrétisation des flux, de type volumes-finis, dite à « deux points », est très couramment utilisée dans les codes de simulation. Ce schéma de résolution se révèle pourtant peu précis sur les interfaces présentant un changement de loi de pression capillaire. Une solution classique pour améliorer la précision sur les flux calculés consiste à ajouter une ou plusieurs inconnues sur les faces du maillage localisées entre deux types de roche [4]. Le travail, réalisé ici, a montré aussi que le simple ajout de mailles fines supplémentaires de part et d’autre des interfaces de changement de roche permet numériquement d’améliorer l’ordre de convergence du schéma « deux-points ». Cette solution ne demande en pratique que très peu de changement à un code mettant en jeu la forme classique de ce schéma. Elle a été également comparée à d’autres formes de raffinement au cours d’une seconde étude [5] et, par rapport à celles-ci, s’est révélée la plus adaptée dans la plupart des cas considérés.
Une méthodologie promise à un bel avenir
La solution développée peut être facilement étendue à la simulation des écoulements polyphasiques (diphasiques voire triphasiques) en milieu poreux, occasionnant ainsi des retombées bénéfiques pour divers cas d’application, comme par exemple le stockage souterrain du CO2. C’est pourquoi les prochaines étapes vont consister à mettre en œuvre ces résultats au sein de la plate-forme de calcul ArcGeoSim développée par IFPEN en partenariat avec le CEA [6, 7].
Références:
1. S. Bassetto, Towards more robust and accurate computations of capillary effects in the simulation of multiphase flows in porous media, Thèse de doctorat de l’Université de Lille (2021).
2. K. Brenner, C. Cancès, Improving Newton's method performance by parametrization: the case of Richards equation, SIAM J. Numer. Anal. 55 (2017), 1760-1785. https://hal.archives-ouvertes.fr/hal-01342386
3. S. Bassetto, C. Cancès, G. Enchéry, Q-H. Tran, Upstream mobility finite volumes for the Richards equation in heterogeneous domains, ESAIM : M2AN 55 (2021), 2101-2139. https://hal.archives-ouvertes.fr/hal-03109483
4. G. Enchéry, R. Eymard, A. Michel, Numerical approximation of a two-phase flow problem in a porous medium with discontinuous capillary forces, SIAM J. Numer. Anal. 43 (2006), 2402-2422. https://doi.org/10.1137/040602936
5. S. Bassetto, C. Cancès, G. Enchéry, Q-H. Tran, On several numerical strategies to solve Richards’ equation in heterogeneous media with finite volumes, preprint (2021). https://hal.archives-ouvertes.fr/hal-03259026
6. G. Grospellier, B. Lelandais, The Arcane development framework, Proceedings of the 8th workshop on Parallel/High-Performance Object-Oriented Scientific Computing 4 (2009), 1-11. https://doi.org/10.1145/1595655.1595659
7. https://github.com/arcaneframework/framework
8 . M.T. van Genuchten, A closed-form equation for predicting the hydraulic conductivity of unsaturated soils. Soil Sci. Soc. Amer. J 44 (1980) 892–898.
Contact scientifique: Guillaume.Enchery@ifpen.fr






