La modélisation des réservoirs souterrains est incontournable pour beaucoup d’applications : gestion des aquifères, stockage de composés ou d’énergie dans le sous-sol, récupération de ressources minérales ou énergétiques comme en géothermie. La modélisation permet de mettre en place une gestion optimale de la ressource tout en minimisant les risques sociétaux et environnementaux. Pour être efficace, cette modélisation doit néanmoins être multi-échelle, aussi les recherches des équipes d’IFPEN sont-elles guidées par cette contrainte.
Modélisation multi-échelle en géosciences
Il est aisé de comprendre la structure multi-échelle des systèmes considérés, par exemple par l’observation d’un affleurement du sous-sol, puis d’extrapoler par la pensée la structure souterraine sous-jacente. L’observation ainsi que des forages et l’analyse géologique/géophysique détaillée confirment l’existence de structures emboîtées dont les échelles varient de l’échelle du pore, typiquement du µm, aux échelles plurikilométriques. Les géologues, géophysiciens et les pétrophysiciens sont capables de fournir des outils de description pertinents à chacune des échelles considérées, mais ceux-ci restent non exhaustifs.
Les spécialistes en géosciences d’IFPEN doivent ainsi idéalement construire des modèles capables de reproduire cette complexité, incorporant les données observées aux différentes échelles, tout en prenant en compte le caractère incomplet des données.
Par ailleurs, ces chercheurs sont vite confrontés avec des modèles qui comptent des dizaines de paramètres d’entrée1. Or il est impossible d’explorer de façon détaillée un espace de grande dimension avec les outils de calcul actuels ou futurs qui sont très rapidement confrontés au « mur de la dimension ». C’est ce « mur » qui justifie les approches de type « plans expérience/réduction de modèles » ou le recours à l’intelligence artificielle, lesquels permettent une réduction drastique du coût de calcul, mais reposent finalement sur une base d’apprentissage fort réduite : au mieux quelques milliers de simulations de référence pour explorer un espace possédant des milliers de dimensions.
Un compromis est donc à trouver entre ces approches de réduction de modèle, et la nécessité de garder une bonne cohérence physique.
1 positions des limites, épaisseurs de couches, porosités, position et trajectoires des puits, débits d’injection ou de production de fluides etc…
Méthodologie du changement d’échelle
Historiquement, l’idée du changement d’échelle précède les approches déjà évoquées tout en les complétant. Il s’agit de réduire à la fois la valeur du coût unitaire et du nombre de degrés de libertés décrivant la dimension cumulée des paramètres2. Pour ce faire, la description du modèle géologique est agrégée en regroupant les paramètres afin de construire un modèle réduit suffisant pour explorer de façon fiable les configurations d’intérêt. Cette démarche se justifie par l’idée que l’intérêt porte essentiellement sur des valeurs moyennes (volumes de fluides, teneurs en minerais, etc.) évaluées sur le volume de la formation considérée. Ceci permet d’obtenir un effet de moyenne analogue à une loi des grands nombres lissant les détails des cas considérés.
2 paramètres qualifiés de contrôlables car raisonnablement connus, voire choisis (position de puits, débits de soutirage) ou dits «incontrôlables » car imposés par la nature, et donc connus avec une certaine incertitude.
Travaux réalisés
L’approche adoptée a consisté à traiter un problème d’écoulement modèle en milieu poreux en combinant une mise à l’échelle déterministe avec une approche stochastique. Ceci a consisté à analyser des résultats de simulations en tirant au hasard plusieurs réalisations possibles d’une «réalité géologique» représentée sous forme d’une carte de perméabilité aléatoire à l’aide de structures générées artificiellement.
Ce travail a été rapporté dans les articles cités en référence, dont voici quelques éléments principaux :
La figure 1 illustre la géométrie typique de la simulation d’un problème d’écoulement en milieu poreux. La géométrie réelle est « maillée » par une grille fine incorporant les détails de la forme des frontières et des discontinuités du domaine, et chaque maille est décrite par un jeu de paramètres issus de données géologiques (porosité, perméabilité…). Une échelle intermédiaire de calcul est ensuite utilisée pour obtenir des résultats fiables, c’est-à-dire sans dégradation importante de la qualité de la représentation des discontinuités ni de celle des données géologiques. La détermination de ce compromis optimal qualité-coût de calcul peut se faire en déterminant des échelles spatiales caractéristiques des solutions du problème simplifié.
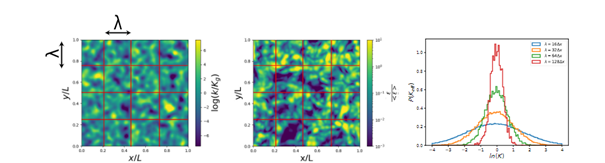
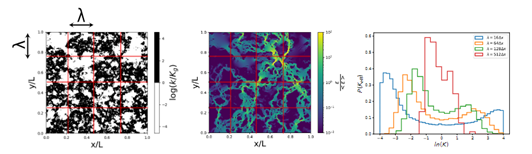
La figure 2 illustre les résultats de post-traitements obtenus par une résolution rapide de l’écoulement sur un milieu aléatoire. Les histogrammes des distributions de perméabilité obtenues par post traitement de la solution à différentes échelles sont fournis sur la figure de droite. La convergence des distributions vers la gaussienne illustre le rôle de la taille du volume élémentaire représentatif. On peut noter que la convergence vers une distribution limite est plus lente lorsqu’on prend en compte une distribution de perméabilité bimodale. Au seuil de connectivité (percolation) le caractère bimodal subsiste à grande échelle et la convergence vers « l’homogène équivalent » devient très lente, car le milieu n’est quasiment plus homogénéisable.
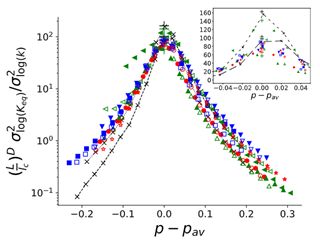
La figure 3 présente l’évolution de la variance de la perméabilité (en Log) en fonction de la distance au seuil de percolation, pour diverses techniques de génération d’images discrètes (bas de la figure 2). Le regroupement des courbes peut permettre d’anticiper rapidement sur un cas précis le régime d’écoulement macroscopique dans lequel se trouve le cas étudié, et les échelles pertinentes d’un problème.
Les résultats de ce travail permettent de mieux comprendre le processus de mise à l’échelle à l’aide d’une utilisation parcimonieuse (post traitement) des résultats de simulation. En utilisant cette méthode, il devient possible de trouver en cours de calcul les échelles pertinentes et les agrégats de paramètres contrôlant les résultats finaux d’intérêt pour les applications. Des approches de ce type seront tout particulièrement mises à profit dans le projet ERC Karst.
Références:
[1] Colecchio, I., Boschan, A., Otero, A. D., & Noetinger, B. (2020). On the multiscale characterization of effective hydraulic conductivity in random heterogeneous media: a historical survey and some new perspectives. Advances in Water Resources, 140, 103594, https://doi.org/10.1016/j.advwatres.2020.103594.
[2] Noetinger, B. (2020). Statistical physics and applied geosciences: some results and perspectives. Comptes Rendus. Physique, 21(6), 539-560, DOI:10.5802/crphys.40.
[3] Colecchio, I., Otero, A. D., Noetinger, B., & Boschan, A. (2021). Equivalent hydraulic conductivity, connectivity and percolation in 2D and 3D random binary media. Advances in Water Resources, 158, 104040, https://doi.org/10.1016/j.advwatres.2021.104040.
Contact scientifique : B. Noetinger









