Le trafic routier urbain est une source significative d’émissions de polluants qui impacte la qualité de l’air. Pouvoir prédire la dispersion de ces émissions représente un enjeu important à la fois pour évaluer les expositions réelles et pour aménager les plans de circulation.
Dans ce but, un travail doctoral a proposé une chaîne de modélisation permettant de simuler les écoulements fortement turbulents à l’échelle micro-urbaine et d’obtenir des cartes spatiales bi-dimensionnelles de concentration de polluants (Figure 1) [1].
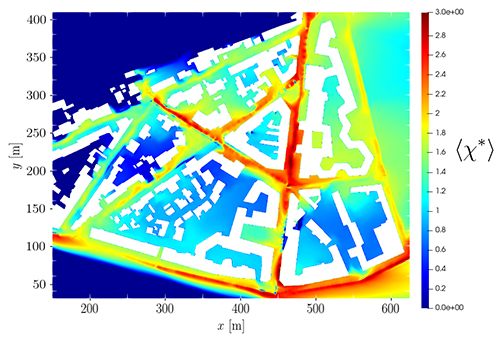
L’élaboration de ces cartes fait intervenir différentes variables dites incertaines (càd non ou mal connues a priori): variables météorologiques (direction θ et force du vent U∞) et variables liées au trafic (volume de trafic q, limitation de vitesse vmax et proportion de véhicules diesel et essence β). Certaines sont plus influentes que d’autres sur les sorties prédites par le modèle et leur identification se fait par le biais de méthodes d’analyse de sensibilité, une des thématiques abordées dans le cadre du consortium CIROQUO2.
Concernant ces méthodes, l’approche classique consiste à calculer un indice de sensibilité usuel (comme les indices de Sobol3) sur une discrétisation de l’espace pour obtenir des cartes de sensibilité. Dans le cadre d’une autre thèse CIROQUO/IFPEN4, une nouvelle famille d’indices de sensibilité adaptée à des sorties de modèles, qui sont non pas des scalaires mais des ensembles, a été proposée [2] et mise en œuvre pour cette application [3]. Au lieu de produire des cartes de sensibilité, cette nouvelle approche caractérise l’influence des différents paramètres d’entrée sur un ensemble aléatoire. Ici, l’ensemble considéré est tri-dimensionnel, avec d’une part les coordonnées spatiales (x,y) et d’autre part le niveau de concentration en polluants, tel que calculé à partir de différentes valeurs des variables incertaines. Ses performances ont été comparées avec des méthodes issues de la littérature : les indices de Sobol (après adaptation aux ensembles) et les indices dits universels qui peuvents’appliquer à tous types de variables.
Les résultats de cette comparaison sont présentés à la Figure 2 et montrent tout d’abord que les différentes approches fournissent des résultats similaires pour ce qui est de classer l’influence des variables d’entrée (ranking). Cependant, la nouvelle méthode proposée permet également de statuer sur le caractère négligeable ou non des variables via un test statistique (screening). Il en résulte une réduction potentielle du nombre de variables à étudier. De plus, les intervalles de confiance obtenus sur les prédictions des indices sont globalement plus faibles qu’avec les autres approches [3].
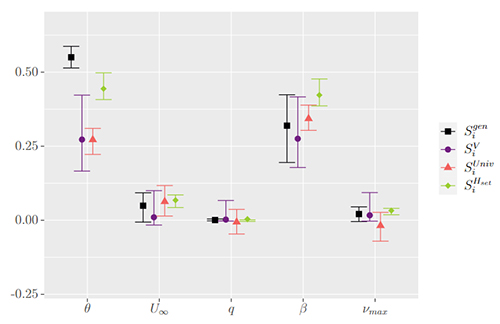
En conclusion, la nouvelle approche proposée permet de statuer quant à l’aspect négligeable ou pas d’une variable, puis de classer les variables restantes par degré d’importance. Enfin, cette nouvelle méthode présente des perspectives intéressantes pour d’autres applications nécessitant de connaître l’influence de variables incertaines au cours d’une optimisation robuste5 [2].
1- Thèse de Mathis Pasquier, Quantification d’incertitudes pour la dispersion turbulente de polluants liés au trafic routier à l’échelle micro-urbaine, Université Aix Marseille, soutenue le 21 Décembre 2023.
2- Consortium Industrie et Recherche pour l’Optimisation et la Quantification d’incertitude pour les données onéreuses, https://ciroquo.ec-lyon.fr/
3- Indice de sensibilité d'une variable de sortie à une variable d'entrée (basé sur une décomposition de variance).
4- Thèse de Noé Fellmann, Analyse de sensibilité des problèmes d'optimisation sous incertitudes, Ecole Centrale Lyon (en cours).
5- C’est-à-dire une optimisation pour laquelle l’ensemble admissible des solutions est défini par des contraintes dépendantes de variables incertaines.
Références :
-
Mathis Pasquier, Stéphane Jay, Jérôme Jacob, Pierre Sagaut. A Lattice-Boltzmann-Based Modelling Chain for Traffic-Related Atmospheric Pollutant Dispersion at the Local Urban Scale. Building and Environment, 2023, 242, pp.110562,
>> 10.1016/j.buildenv.2023.110562
-
Noé Fellmann, Christophette Blanchet-Scalliet, Céline Helbert, Adrien Spagnol, Delphine Sinoquet. Kernel-based sensitivity analysis for (excursion) sets. 2023.
>> hal-04094561v3
-
Noé Fellmann, Mathis Pasquier, Céline Helbert, Adrien Spagnol, Delphine Sinoquet, Christophette Blanchet-Scalliet, Sensitivity analysis for sets: application to pollutant concentration maps. 2023
>> hal-04312097
Contacts scientifiques : adrien.spagnol@ifpen.fr et Delphine Sinoquet






