Le calcul haute performance ou HPC (High-Performance Computing) est un champ scientifique qui concerne à la fois les mathématiques et l’informatique, et dont l’application touche de nombreux domaines tels que l’énergie, la mobilité ou l’environnement. Dans tous ces domaines, le besoin de simuler des phénomènes physiques à grande échelle s’appuie en effet sur des modèles mathématiques qui sont gourmands en temps de calcul et en espace de stockage.
Le but du HPC est alors d’optimiser l’utilisation des ressources - machines, logiciels, algorithmes, méthodologies de développement, etc. - pour permettre de traiter, de manière précise et rapide, des problèmes complexes et massifs1 issus d’applications très variées.
Ces simulations se font à l’aide de supercalculateurs2 qui disposent de CPU3 embarquant un grand nombre de cœurs4 (de 18 pour Ener440 à 64 pour Irene et 96 pour Adastra).
Malgré leur puissance intrinsèque, la question se pose désormais de calculer plus efficacement avec ces machines, leurs processeurs multi-cœurs, leur hiérarchie mémoire complexe et leurs unités de calcul sophistiquées. Cela concerne notamment la synchronisation rapide et efficiente des cœurs.
La synchronisation en mémoire partagée est un sujet ancien et de nombreuses méthodes ont été proposées, que l’on retrouve dans différents compilateurs utilisés en HPC. Pour la parallélisation classique d’un code en mémoire partagée, la synchronisation des cœurs vise d’une part à organiser le bon ordre des calculs (par l’insertion de barrières5) et d’autre part à garantir la capacité à combiner les résultats produits par l’ensemble des cœurs (pour pouvoir les réduire en un seul résultat). Dans tous les cas, le temps qui y est consacré doit être minimal, mais, pour des processeurs avec un grand nombre de cœurs, le surcoût en temps de calcul lié à l’utilisation intensive de ces mécanismes de synchronisation standard de compilateurs (comme GCC ou Intel) est significativement élevé. Ils peuvent même devenir des goulots d’étranglement des performances pour les codes massivement parallèles.
La Figure 1 illustre la barrière de synchronisation Extended-Butterfly, proposée dans le cadre d’une thèse6 réalisée à IFPEN, pour des codes parallèles en mémoire partagée afin de répondre à cette problématique. Son originalité réside dans la mise en place d’une synchronisation par groupes7 sur deux niveaux : une synchronisation intra-groupe puis inter-groupe [1]. Le nombre d’étapes nécessaires à la synchronisation dépend du logarithme du nombre de groupes et cela conduit à ce que pour nos 7 cœurs 4 étapes soient suffisantes pour les synchroniser.
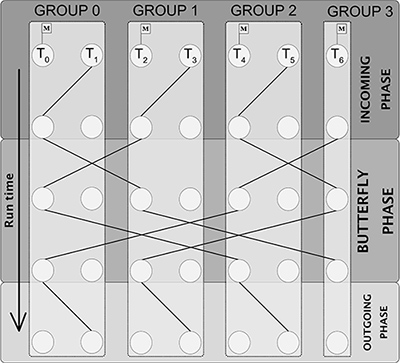
Les traits foncés symbolisent l'envoie d'une notification d'un cœur à un autre.
La barrière se fait en 3 étapes :
- une étape d’entrée,
- une étape dans Butterfly
- et une étape de sortie.
Seuls les cœurs représentés avec un drapeau sont autorisés à entrer dans la phase Butterfly pendant que leur partenaire attend leur notification de la phase de sortie.
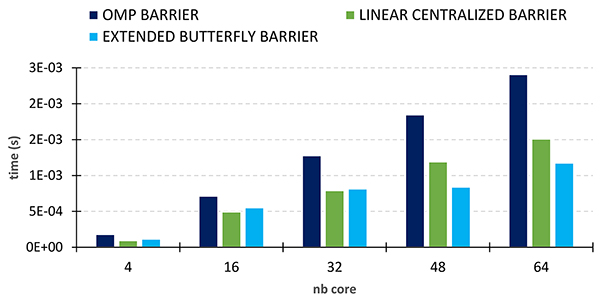
Les résultats des tests de performance pratiqués (Figure 2) montrent que cette barrière (histogramme bleu clair) nécessite un temps de synchronisation (ou latence) plus faible que la barrière de l’interface de programmation OpenMP avec les compilateurs GCC (histogrammes bleu foncé).
Notre barrière Extended Butterfly a ensuite été utilisée comme support pour les opérations de réduction. Notre méthode Extended Butterfly Reduction est jusqu’à 4 fois plus rapide (pour 64 cœurs) que la réduction d’OpenMP avec GCC sur le processeur AMD Milan (Figure 3).
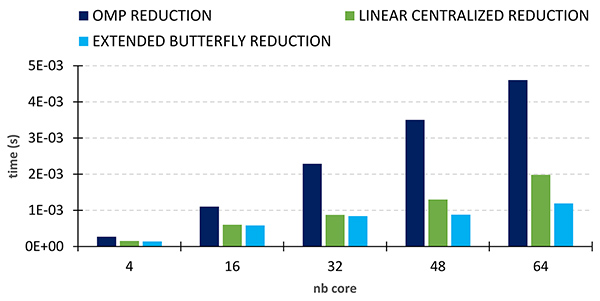
La barrière et la réduction Linear Centralized (les histogrammes en vert) représentent les anciennes méthodes mises en place dans MCGSolver8, la librairie de solveurs linéaires massivement parallèle d’IFPEN. Là aussi, les nouvelles méthodes employées dans Extended-Butterfly conduisent à des performances notablement meilleures pour un nombre de cœurs supérieurs à 40.
En résumé, la puissance de calcul apportée par les nouveaux processeurs, grâce notamment aux grands nombres de cœurs qu’ils embarquent, pose la question de leur exploitation optimale. Notre nouvelle méthode Extended-Butterfly propose une approche efficace pour répondre à cette problématique, en gagnant sur plusieurs aspects au niveau de la synchronisation des cœurs. Ces méthodes ont été intégrées dans la librairie MCGSolver.
1- Utilisant de grandes quantités de données.
2- Comme Ener440 (IFPEN), Irene (TGCC) ou Adastra (GENCI-CINES), la machine la plus récente qui figure dans le top 3 du Green500 de 2022.
3- Unité centrale de calcul (Central Processing Unit).
4- Un cœur est un ensemble de circuits capables d'exécuter des programmes de façon autonome.
5- Action visant à suspendre le calcul de certains cœurs en attendant les autres.
6- A. Mohamed El Maarouf, Factorisation incomplète et résolution de systèmes triangulaires pour des machines exploitant un parallélisme à grain fin. Université de Bordeaux, 2023. HAL : tel-04429547 >> https://theses.hal.science/tel-04429547
7- Notion algorithmique introduite dans le cadre de ce travail.
8- Multi-Core multi-Gpu Solver.
Référence :
-
A. Mohamed El Maarouf, L. Giraud, A. Guermouche, T. Guignon, Combining reduction with synchronization barrier on multi-core processors, CCPE Journal, 2023.
>> DOI : 10.1002/cpe.7402
Contacts scientifiques : aboul-karim.mohamed-el-maarouf@ifpen.fr et thomas.guignon@ifpen.fr






