Le transport de polluants dans les sols est directement tributaire de l'hétérogénéité du milieu présent (topologie, structure, etc.), lequel est par ailleurs fortement impacté par certaines activités humaines comme l’agriculture, l’activité industrielle ou encore les mines. La description précise de ce phénomène, à toutes les échelles de temps, peut ainsi paraître complexe. Cependant elle est importante pour répondre à des enjeux majeurs, comme le traitement efficace des eaux usées, ou l’accès du plus grand nombre à de l’eau potable de bonne qualité. Dans ce contexte, les chercheurs IFPEN ont travaillé sur des méthodes pour mieux comprendre comment les polluants sont transportés dans le sous-sol.
Un transport de polluants impacté par l’hétérogénéité du milieu
Les régimes de transport de polluants (transitoire et asymptotique), ainsi que le temps mis pour atteindre un endroit critique (par exemple un aquifère ou un puits) dépendent fortement de l'hétérogénéité sous-jacente du champ de perméabilité. De plus, dans le cas de la rétention de polluants, le transport est également caractérisé par une cinétique d'échange qui dépend des propriétés locales du sol. C’est pourquoi les temps de rétention sont eux aussi spatialement hétérogènes.
Deux approches pour la modélisation du transport de solutés
Dans ce travail, les chercheurs IFPEN se sont intéressés à l'influence d’une perméabilité et de temps de rétention hétérogènes sur les régimes transitoire et asymptotique de transport d’espèces. En effet, le transport en régime transitoire ne peut pas être décrit par une équation de transport classique (Equation Advection-Diffusion). Cette équation devient valable seulement dans le régime asymptotique.
Dans une première partie, les chercheurs ont simulé ce transport dans un milieu poreux hétérogène bidimensionnel. Un modèle Mobile-Immobile1 a été utilisé pour décrire l'impact sur le transfert global des solutés du transfert de masse entre les parties mobiles et immobiles du milieu. Ce problème a été résolu en utilisant une méthode de Lattice Boltzmann sur réseau2 [1].
1 Ce modèle se distingue du modèle de transport classique par le fait qu’il sépare dans la même maille de simulation la région fluide en régions mobile (écoulement et diffusion) et immobile (stagnante) avec un transfert entre la partie mobile et la partie immobile. Ce transfert suit une équation cinétique d’ordre 1.
2 Méthode numérique permettant de résoudre l’équation de Navier-Stokes et l’équation d’advection-diffusion à l'aide d'un schéma de collision-propagation.
Dans une seconde partie, un nouveau modèle de marche aléatoire unidimensionnel (continuous time random walk, CTRW) a été mis en œuvre par les chercheurs pour déterminer ces comportements de transport à grande échelle. Le modèle est basé sur un modèle de Markov spatial3 pour les vitesses des particules, lequel couple le transport advectif-dispersif et le transfert de masse hétérogène par un processus de Poisson4. Ce modèle, qui se situe à une échelle spatiale et temporelle supérieure, peut être entièrement paramétré par les statistiques de perméabilité et d’écoulement (sans paramètre d'ajustement) et permet de réaliser des simulations numériques plus longues pour atteindre les régimes asymptotiques.
3 Processus stochastique décrivant le passage d’un état à un autre.
4 Processus stochastique qui permet de décrire des événements aléatoires avec une certaine probabilité dans le temps.
Sous l’hypothèse d’une relation non-linéaire entre la perméabilité locale K et le temps d'échange local τ, les chercheurs ont étudié l'impact du nombre de Damköhler (Da, rapport des échelles de temps d'advection et de rétention) sur l'évolution spatiale du champ de concentration en solutés.
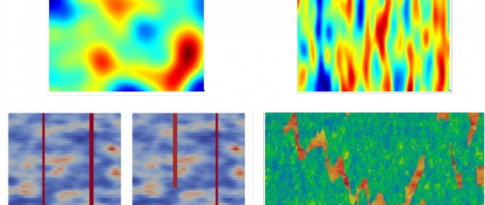
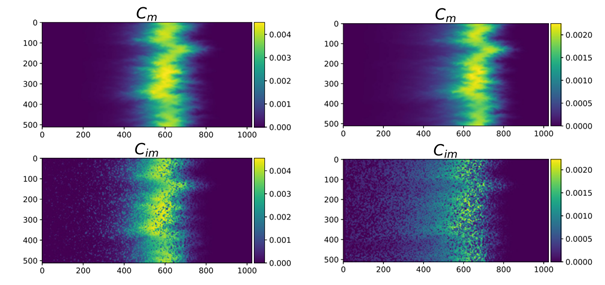
La Fig. 1 montre des champs de concentration pour différentes valeurs de Da [2]. Les deux champs de concentration mobile sont très similaires, alors que des différences importantes peuvent être observées dans les champs de concentration immobile. Dans le cas d'un Da faible, il y a un plus grand nombre de régions appauvries (bleu foncé) au niveau du front. Par ailleurs, d'autres régions de concentration plus élevée peuvent encore être observées loin derrière le front. Ces deux effets résultent de l’hétérogénéité dans le temps de rétention et ces régions correspondent en effet à des grandes valeurs de ce paramètre.
Grâce aux simulations numériques CTRW, les chercheurs ont également montré que le temps nécessaire pour atteindre les régimes asymptotiques dans les milieux hétérogènes est en moyenne deux ordres de grandeur plus élevé que pour le cas d’un milieu poreux homogène.
Une forte variabilité du temps de rétention des polluants
En conclusion, les chercheurs ont montré, à partir de simulations numériques, que des concentrations de polluants peuvent parfois rester sur des temps très longs dans le sol. Ceci s’explique par l’existence des zones stagnantes (régions bleues, Fig .1) dotées d’une haute valeur de temps de rétention. Ces zones stockent et libèrent des polluants sur des durées très longues.
De plus, les simulations CTRW ont montré que les régimes de transport transitoire peuvent être importants, mais leur description correcte nécessite des modèles plus élaborés. Finalement, les résultats permettent d’expliquer potentiellement les comportements spécifiques observés expérimentalement et qui ne peuvent pas être modélisés par une équation de transport classique.
Pour une prise en compte de milieux plus complexes
Pour faire suite à cette étude, une tâche difficile et ambitieuse reste à entreprendre : simuler le transport des polluants dans des structures plus complexes, notamment anisotropes ou stratifiées, afin de rendre compte de la grande hétérogénéité des milieux géologiques.
[1] Talon L., Martin J., Rakotomalala N., Salin D. and Yortsos Y., 2003, Lattice BGK simulations of macrodispersion in heterogeneous porous media, Water Resources Research. https://doi.org/10.1029/2002WR001392
[2] Talon, L., Ollivier-Triquet, E., Dentz, M., Bauer, D., 2023. Transient dispersion regimes in heterogeneous porous media: On the impact of spatial heterogeneity in permeability and exchange kinetics in mobile–immobile transport. Advances in Water Ressources. https://doi.org/10.1016/j.advwatres.2023.104425
Contact scientifique : daniela.bauer@ifpen.fr
Vous serez aussi intéressé par
Modèle adaptatif pour la simulation d'écoulements en milieux poreux hétérogènes
Le calcul des écoulements d’eau et de gaz dans les milieux rocheux complexes et hétérogènes est au cœur des solutions technologiques en lien avec les enjeux climatiques et énergétiques actuels, ...
VS4 - Nouvelle voie numérique pour la caractérisation de matériaux poreux virtuels
A l'intérieur des matériaux poreux, les phénomènes physico-chimiques tels que le transport de matière, les réactions catalytiques et les effets capillaires sont fortement influencés par la géométrie des réseaux de pores, c’est-à-dire le degré de porosité, la distribution de taille des pores et leur connectivité. (....) IFPEN et Saint Gobain Research Provence ont choisi d’appréhender ce problème de manière différente, en explorant une nouvelle voie numérique...